曼-惠特尼U检验Mann-Whitney U test

检验除总体均值外完全相同的两个总体的均值是否有显著差别的秩和检验。由曼(Henry Berthold Mann, 1905—2000)和惠特尼(Donald Ransom Whitney)1947年提出。具体步骤是： (1) 将两组数据混合，并按照大小顺序编排等级，最小数据的等级为1，其次数据的等级为2，以此类推(若几个数据相等，则以这几个数据应得等级的平均值作为其等级);(2) 分别计算两样本的等级和W₁、W₂;(3) 计算曼-惠特尼U检验统计量：

U₁＝n₁n₂+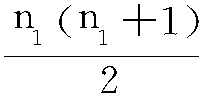-W₁
U₂＝n₁n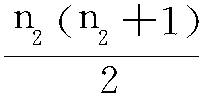₂+-W₂

其中，n₁为第一个样本容量，n₂为第二个样本容量。当n₁和n₂都大于或等于10时，随机变量近似服从正态分布。在原假设为真的情况下，随机变量U的均值和方差分别为：

E(U)=,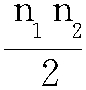
D(U)=;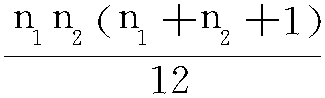

(4) 作出判断。选择U₁和U₂中最小者与临界值U_α(查曼-惠特尼U检验表获得)比较，当Uα时，拒绝H₀（即两总体均值没有显著差异），接受H₁（即两总体均值有显著差异）。反之，则接受H₀，拒绝H₁。