普遍二次曲面不变量的完全系统pubian erci qumianbubianliang de wanquan xitong

对于普遍二次曲面F (x,y,z)≡ax² +by² + cz² + 2fyz+ 2gzx + 2hxy+2ux+2vy+2wz+d=0 (a²+b²+c²+f²+g²+h²≠0)有

是移轴和转轴下的不变量.

和

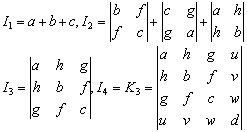
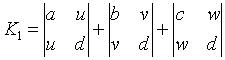
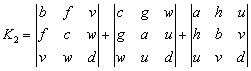
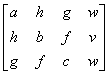是转轴下的不变量. 且当矩阵A=的秩是1时，K1是移轴下的不变量；秩是2时，K₂是移轴下的不变量.I₁,I₂,I₃和I₄叫做普遍二次曲面F (x,y,z)=0的基本不变量，K₁和K₂叫做条件不变量或半不变量.这六个不变量组成普遍二次曲面不变量的完全系统.利用它们可以完全确定曲面的形状，但不能确定曲面的位置.普遍二次曲面F (x,y,z)=0所表示的轨迹可用I₁,I₂,I₃,I₄,=K₃及K₁,K₂判别如下表：

型的检验	判 别 标 志		曲 面名 称
中心型 I3≠0	I2>0 I1·I3>0	K3<0	❶椭圆面
		K3>0	❷无实轨迹 （虚椭圆面）
		K3=0	❸点 （虚锥面）
	I2≤0 或I1·I3≤0	K3>0	❹单叶双曲面
		K3<0	❺双叶双曲面
		K3=0	❻二次锥面
第一类无心型 I3=0,K3≠0	I2>0 (或K3<0)		❼椭圆抛物面
	I2<0 (或K3>0)		❽双曲抛物面
第一类多心型 I3=0,K3=0, I2≠0	I2>0	I1·K2<0	❾椭圆柱面
		I1·K2>0	❿无实轨迹 （虚椭圆柱面）
		K2=0	(11)直线 （一对相交虚平面）
	I2<0	K2≠0	(12)双曲柱面
		K2=0	(13)一对相交平面
第二类无心型 I3=0, K3=0 I2=0, K2≠0			(14)抛物柱面
第二类多心型 I3=0,K3=0 I2=0, K2=0		K1<0	(15)一对平行平面
		K1>0	(16)无实轨迹 （一对平行虚平面）
		K1=0	(17)一对重合平面