时间序列模型time series models

运用随机过程理论和数理统计方法研究时间序列的数学模型。时间序列是指按时间顺序排列的同一变量的一组观察值。时间序列模型中把时间作为影响研究对象发生变化的各种因素的总代表。根据具体问题用适当的单位(如年、月或小时)计量时间，以t表示。它着重研究数据序列的相互依赖关系。用时间序列模型进行预测，属于历史资料引申性预测，具有所用历史数据较少，易于收集的优点，因而得到广泛应用。常用的时间序列模型见下图。

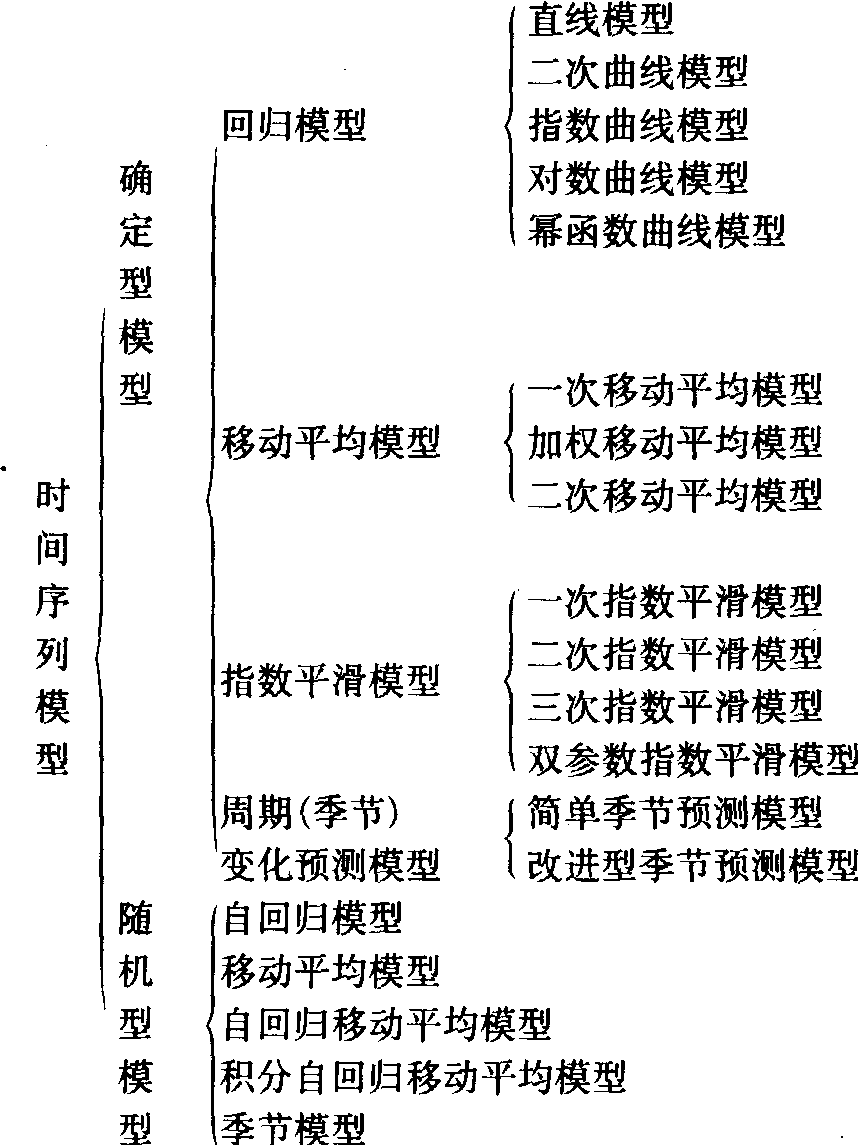
常用的时间序列模型

确定型模型 用时间t的确定函数描述问题的模型。
回归模型 参见回归模型。
移动平均模型 用移动平均法建立的模型。移动平均法是在时间序列上，由第一个数据开始，按一定跨越期每次后移一个时间单位，计算跨越期内各数据点值的平均数，得到新时间序列的方法。跨越期由分析者按问题情况选定。移动平均模型中常用的有一次移动平均模型、加权移动模型和二次移动平均模型。
一次移动平均模型 又称简单移动平均模型。其计算式为：

式中 t为时间；M_t⁽¹⁾是t时刻的一次移动平均数；N跨越期数；X_t为t时刻统计数。式(1)也可写成递推形式：

当N=1时，M_t⁽¹⁾＝X_t,仍为原时间序列；当N=t时，M_t⁽¹⁾为整个时间序列的算术平均数。当N取值较大时，移动平均数对干扰的灵敏度较低，比较平稳保险，但适应新水平的时间要长，易滞后于可能的发展趋势；相反，N取值较小时，模型对数据变化反应灵敏，适应新水平的时间短，但可能由于对随机因素干扰反应过度而造成错觉，误把假象当规律。根据经验，一般取N=5～200之间，如果数据点多，或者预测周期长，N可取大些，否则N应取小些。一次移动平均法一般仅适用于近乎水平趋势的时间序列数据，局限性较大。
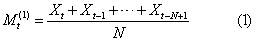
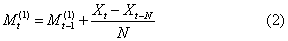
加权移动平均模型 对跨越期中各数据赋予不同权数作移动平均计算而建立的模型。其计算式为：

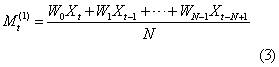
式中 W₀,W₁…W_N-1为权系数，应满足条件W_t＝N，一般对近期数据赋予较大的权数。加权移动平均模型常用于原始时间序列有上升或下降的线性趋势的情况。
二次移动平均模型 对一次移动平均得到的时间序列再做移动平均，得到更平滑的时间序列模型。其计算式为：

式中 M_t⁽²⁾为t时刻的二次移动平均数，一般不直接用来进行分析和预测，而是用它来建立二次移动平均预测模型：

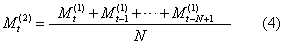
式中 T为由预测起点时刻t到需要预测的时刻t+T之间的时间单位的数；_t+T为t+T时刻的预测值；a_t、b_t为平滑系数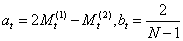，(M_t⁽¹⁾-M_t⁽²⁾)。二次移动平均模型适用于具有线性趋势的时间序列的分析和预报。
指数平滑模型 对时间序列的每个数据，按新老不同，分别赋予按指数规律递减的权数而建立的模型。也称指数加权移动平均模型。是移动平均模型的改进和发展。常用的有一次指数平滑模型、二次指数平滑模型和三次指数平滑模型。
一次指数平滑模型 其计算式为：

S_t⁽¹⁾＝αX_t+(1-α)S_t-1⁽¹⁾ (6)

式中 S_t⁽¹⁾、S_t-1⁽¹⁾分别为t时刻和t-1时刻的一次指数平滑值；α为权系数，0<α<1，一般取α =0.01～0.50。α取值较大时，平滑值对新情况的反应较迅速，但α过大时，可能对随机影响反应过度；α取值较小时，平滑值对新情况反应较缓慢。展开式(6)可得：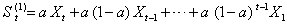

式(7)说明以下三点：❶时间序列中各数据的权系数不同，离当前时刻愈远的数据的权数愈小，因而对平滑值的影响也愈小；离当前时刻愈近的数据的权数愈大，对平滑值的影响也愈大；
❷S_t⁽¹⁾是以前一时刻的值S_t-1⁽¹⁾为起点而算得的，具有递推性，所以可减少数据储存量；
❸计量S_t⁽¹⁾需给出初始值S₀⁽¹⁾。当序列数据较多时，S₀⁽¹⁾的影响很小，常取S₀⁽¹⁾＝X₁；当序列数据较少时，(例如不足15个数据时),S₀⁽¹⁾对S_t⁽¹⁾的影响将不可忽略，需用其他方法确定，较简单的一种方法是取数据序列前几个数据值的算术平均值作为初始值。一次指数平滑模型仅适用于近乎水平趋势的时间序列的分析和预测。
二次指数平滑模型 对一次指数平滑得到的时间序列再做指数平滑而得到的模型。其计算式为：

S_t⁽²⁾＝ αS_t⁽¹⁾+(1-α )S_t-1⁽²⁾(8)

式中 S_t⁽²⁾、S_t-1⁽²⁾分别为t时刻和t-1时刻的二次指数平滑值。S_t⁽²⁾一般不直接用来进行分析和预测。而是通过它来建立二次指数平滑预测模型：

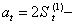
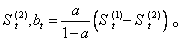式(9)与式(5)有相同的形式，均用于具有上升或下降线性趋势的时间序列的分析和预测。但参数a_t、b_t的计算式不同。式(9)中a_t、b_t的计算式为初始值S₀⁽²⁾的确定方法与S₀⁽¹⁾相同，通常取S₀⁽²⁾＝S₀⁽¹⁾。
三次指数平滑模型 对二次指数平滑得到的时间序列再做指数平滑而得到的模型。其计算式为：

S_t⁽³⁾＝αS_t⁽²⁾+(1-α)S_t-1⁽³⁾(10)

式中 S_t⁽³⁾、S_t-1⁽¹⁾分别为t时刻和t-1时刻的三次指数平滑值。S_t⁽³⁾一般也不直接用来进行分析和预测，而是通过它来建立三次指数平滑预测模型。

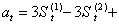
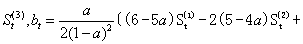
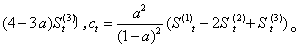式中 参数a_tb_t、c_t的计算式为：初始值S₀⁽³⁾的确定与S₀⁽¹⁾相同，且常使S₀⁽³⁾＝S₀⁽²⁾＝S₀⁽¹⁾。三次指数平滑模型用于具有二次曲线变化趋势的时间序列的分析和预测。
季节变化预测模型 对具有季节性变化特点的时间序列进行分析和预测的数学模型。常用的是简单季节预测模型。
简单季节预测模型 它是将时间序列中的长期趋势变化用线性模型_t＝a+b_t表示(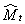称为趋势估计值)，然后乘一个表示季节性变动的季节系数估计值F_t+T而建立起来的模型。即

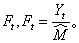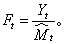系数a、b可用回归法或二次指数平滑法求得。F_t+1的求法是：先求出各时刻的季节系数它是样本观测值Y_t与趋势估计值_t之比。为消除随机影响，取与t+T时刻相对应的各季节系数的算术平均值作为F_t+T。例如：现有某农产品销售额二年半的统计数据。数据呈现季节性变化特点。现在要预测下年第一季度的销售额。这个问题的时间单位为“季”。二年半共有10个季度，t=1为第一年第一季度，按这个时间序列的数据。用回归法得到a、b值，可以算出相应的10个趋势估计值_t(t=1,2，…，10)和10个季节系数其中t=1，5，9的值分别为第一年，第二年和第三年第一季度的值。以第三年第二季度为预测始点，此时t=10，对下年第一季度做预测点，此时t+T=10+3=13(T=3季)于是得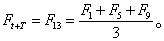

随机型模型 研究由随机过程产生的时间序列的模型。这种时间序列中某个值的出现具有不确定性，但整个时间序列却具有统计规律性，具有代表性的是鲍克斯——詹金斯(Box-Jenkins，称简B-J)模型。B-J模型有五类：自回归模型，移动平均模型，自回归移动平均混合模型，积分自回归移动平均模型和季节模型。
自回归模型的一般公式为：

式中 当前值Y_t是过去观察值Y_t-1,Y_t-2，…Y_t-p的回归，ε_t是误差项，式中含有p个未知参数φ₁,φ₂，…， φ_p，故称为p阶自回归过程，简写成AR(p)。实际中经常使用的是AR(1)、AR(2)模型。
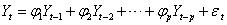
移动平均模型的一般公式为：

Y_t＝ε_t-θ₁ε_t-1-θ2ε_t-2-…-θ_qε_t-q

式中 当前值Y_t是各期的误差值ε_t,ε_t-1，…，ε_t-q的线性组合，含有q个未知参数θ₁,θ₂，…，θ_q，又由于随机变量实际取值有正有负，其线性组合有互相抵消和平均作用，故称为q阶移动平均模型，简写成MA(q)。常用的也是低阶MA模型，即MA(1)、MA(2)模型。
自回归移动平均混合模型的一般公式为：

该模型简称为ARMA(p,q)模型。实际应用中p,q很少超过2。上式表明，AR(p)模型与MA(q)模型只不过是ARMA(p,q)模型的特例，即分别对应q=0,p=0的情况。
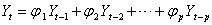
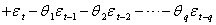
上述三类模型仅限于描述平稳序列，而在实际应用中遇到的时间序列往往是非平稳的。时间序列的不平稳性是多种多样的，然而在经济和管理中遇到的时间序列常常呈现一种特殊的非平稳性，即齐次非平稳性。对这样的序列，只要对它们进行一次或多次差分，就可以将其转换成平稳序列，即可用积分自回归移动平均模型来描述。该模型可简写为ARIMA(p,d,q),d表示差分阶数。大多数时间序列都可以用p, d,q不超过2的ARIMA模型描述。
对于存在季节性的时间序列，可使用B-J季节模型，用季节差分的方法把原序列化成平稳序列，消除其季节性影响。
随机型时间序列有多种类型。由于p,d,q的不同，每一种类型实际上是一个模型族。因此要根据已知统计数据，从基本模型族中选择一个和预测目标的实际过程等价的模型结构，即进行模型识别，确定模型的结构和层次。模型识别是以时间序列的自相关函数和偏相关函数估计为主，直观检验为辅，两者结合的方法进行。
当时间序列的模型结构和阶次确定后，就要估计模型中参数φ₁,φ₂，…φ_p,θ₁,θ₂，…θ_q，随着模型结构、统计特性和预测精度要求不同，估计的方法也不同，常用的有矩估计，非线性最小二乘法估计，逆函数法等。
为了判断所获得的模型是否适当，还要根据数理统计的有关方法进行模型检验。由最终获得的时间序列模型，可以导出最小均方差意义下的预测值和置信区间。