无理数wú lǐ shù

无限不循环小数。1931年《英汉对照百科名汇》：“Irrational number，无理数。”

有理数←→无理数yǒu lǐ shù ← → wú lǐ shù

有理数：正负整数、正负分数和零的统称。
无理数： 不循环的无限小数。如。
【例】 不循环和无限小数又是一种不同于整数和分数的数，称为无理数。(《初等数学》编写组： 《代数》) 有理数是由整数、有限小数和循环小数所组成。（同上）

无理数

无限不循环小数。如,π（圆周率）都是无理数。人们首先有了自然数（不包括零）的概念，而后才是整数和有理数的概念。古希腊人发现，正方形的对角线长度与边长之比不是有理数。严格定义无理数的方法不止1种。

无理数wulishu

无限不循环小数.由于任何有限小数和无限循环小数都可转化为有理数，反之，每个有理数都可表示为有限小数或无限循环小数，所以无限不循环小数是有理数集以外的一种新的数.
无理数是由于人们对度量的需要而产生的.设正方形的边长为1，以正方形的边去度量正方形的对角线，据勾股定理，对角线的长l应满足l2=2.但又证明了任何有理数的平方不等于2，所以对角线的长l不能表为有理数，为了用数表示任意线段的长，于是引进新的数，即无理数.表示上述对角线长的数就是无理数，它是无限不循环小数1.414213….
由于数的理论发展需要，对于无理数还引进了更一般和更严格的定义.参见“实数”.

无理数Wulishu

人类对无理数的认识与探索，是数学史上最为曲折漫长的过程之一。
最早被涉及的无理数是开方不尽数。巴比伦人曾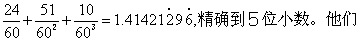显然没有认识到开方不尽数的内在性质。此外，巴比伦人和埃及人也都给出过圆周率的一些近似值，但那完全是从几何意义上考虑的，与无理数的概念并没有什么关系。
最早对开方不尽数的深刻性质有明确认识的是古希腊的毕达哥拉斯学派。人们现在常常把无理数定义为“无限不循环小数”，而这种观点完全是16世纪以后的事情。最初无理数是指那些既不是整数、又不能表示成两个整数之比的数。毕达哥拉斯学派起初认为，世间的一切数量关系都不外乎整数或整数之比。但是，在他们得到了著名的毕达哥拉斯定理（即勾股定理）之后，却由此导出： 单位正方形的对角线与其边长之比不能表示为两个整数之比，用今天的话来说就是： 不是有理数（即整数或分数）。这一事件大约发生在公元前6世纪末至前5世纪初，它导致了数学史上影响极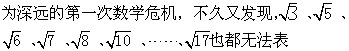
示为两个整数之比，希腊人最初难以承认它们是数，称之为αλoγos或αρρητοs，即不能表达或没有比，后一词后来演变为拉丁文形容词irrationalis以及英文irra_tional, 本义都是没有比。1857年， 中国数学家李善兰与英国人伟烈亚力合作译出了欧几里得《几何原本》的后9卷，在其中，rational和irrational分别被译为“有比例”、“无比例”，1872年，华蘅芳与英国人傅兰雅合译《代数术》，将这两个词分别译为“有理”、“无理”， 不久传入日本， 从此沿用至今。
公元前4世纪，古希腊数学家欧多克斯创立了一套新的、完整的比例理论，巧妙地回避了无理量所涉及到的逻辑困难。此之略早，泰阿泰德(Theaetetus)对当时已经发现的根式无理数作了分类。这些内容后来都被欧几里得收入了《几何原本》。此后，希腊人在许多场合使用无理数，但一般不接受它们作为问题的解，更未能进一步探讨它们的逻辑基础。
中国古代数学中很早就运用了开方不尽数。《九章算术》中将二次不尽根及三次不尽根均称为“不可开”，并探讨了它们的运算，公元三世纪，刘徽创立了十进分数来逼近这两类不尽根。但在中国古代数学中未能对开方不尽数的性质作进一步的探讨， 它们被不加区别地与整数、分数一起使用，而从未有人担心过它们的逻辑基础，在印度和阿拉伯，情况也是类似的。阿拉伯人虽然知道古希腊数学中对两个量是否可公度(即，存在第三个量，使前两个量同时是它的整倍数)的区别，但并不认为这有多么重要。
在欧洲，自文艺复兴以后，数学中使用的无理数越来越多，由于无理数的严格理论始终未能建立，因而引起了数学家的长期担忧与争论，一方面，许多数学问题不使用无理数就得不到结果，另一方面，当用十进小数去表示无理数时，不仅没有一个有限的形式，而且往往毫无规律可循， 无法准确地掌握。因此， 1544年德国数学家施蒂费尔说： “正如无穷大的数并非数一样，无理数也不是一个真正的数， 而是隐藏在一种无穷迷雾后面的东西。”在著名的数学家中，斯台文、笛卡尔、沃利斯(Wallis, J.)都认为无理数是独立的数，而帕斯卡、巳罗(Barrow)、牛顿都认为无理量仅仅在几何上才有意义。
18世纪， 对于无理数在理论上虽无重要进展， 但欧拉证明了e和e²是无理数，兰伯特(Lambert)证明了π是无理数， 勒让德证明了π²是无理数， 并猜测π可能不是任何有理系数多项式方程的根， 这导致了对无理数的分类。
经过文艺复兴以后几百年的探索， 1872年，三位德国数学家在同一年各自独立发表了建立在有理数系基础上的、在逻辑上严格的无理数理论。其中，戴德金是从连续性入手，借助了著名的 “戴德金分割”；康托尔是从完备性入手，借助了有理数的基本序列；外尔斯特拉斯则是利用了有理数的递增有界序列。三个人的工作都与无穷运算，无穷集合联系了起来，而且本质上是等价的。在19世纪中期，还有其他一些数学家对无理数理论作了有价值的探讨。实际上，无理数理论的创立， 是自从公元前500年左右不可公度比被发现之后2000多年来数学家们艰苦探索的结果， 特别是17世纪微积分创立以后对数系的逻辑基础不断探索的结果。
由于无理数的理论是以有理数概念为基础的， 在无理数理论建立之后， 人们加紧了对有理数理论的研究，到1889年，皮亚诺不仅以自然数概念为基础建立了严格的有理数理论， 而且通过引入关于自然数的5条公理，建立了自然数的严格的、公理化的理论系统。至此， 无理数的理论终于有了稳固而严格的基础。
然而，即使在今天，关于无理数也仍然有许多理论问题等待着人们继续探索。

无理数

irrational number