方程fāngchéng

数学上指含有未知数的等式。如x+2=5,x-1=y+3。也说方程式。

029 方程

一次联立方程(线性方程组)的古称。中国古代数学名著《九章算术》曾以“方程”为题设专章讲述。“方程”章共18个题目，未知数最多的达5个。该章给出了一次联立方程的普遍解法。古代以算筹表示一次联立方程。即将各项系数依次用算筹列出，每一方程中各系数自上而下，各方程自右而左，形如方阵，而未知数不以符号表出。这类似于方程组各系数构成的矩阵。然后用“递乘”、“直除”的方法解之。与现今初等代数中的消元法基本相同。实际上就是分离系数法、加减消元法。已经具有现代数学中矩阵的加法变换、消元变换的雏形。这是中国古代数学的重大成就之一。在世界数学史上具有非常重要的意义。欧洲直到16世纪才有加减消元法，17世纪才由莱布尼兹(G.W.Leibniz)、贝祖(.Bézout)逐步建立起线性方程组的一般理论。

方程fangcheng

含有未知数的等式叫做关于这个（或这些）未知数的方程，简称方程.方程中的未知数叫做方程的元.含有几个未知数的方程就叫做几元方程.例如，关于x的方程ax=b，就是以x为未知数的一元方程.等式F₁(x,y,z)=F₂(x,y,z)就表示一个以x,y,z为元的三元方程.
能够使方程左右两边的值相等的未知数的值，叫做方程的解.多元方程的解是一组未知数的值.如x=2,y=1是二元方程2x-y=3的一个解.
一元方程的解也叫做方程的根.如果一个方程的全体根中有几个根相等，那么这几个根叫做重根.例如方程x3(x-1)²(x+3)=0，它的根是x₁＝x₂＝x₃＝0,x₄＝x₅＝1,x₆＝-3.那么“0”就是它的三重根，“1”就是它的二重根，“-3”不是重根，可以称之为单根.一般只对整式方程研究重根问题.
一个方程的解的全体所组成的集合，叫做这个方程的解的集合，简称解集.若方程无解，解集就是空集.无解的方程叫做矛盾方程，故矛盾方程的解集是空集.
求出方程的所有的解或判断方程无解的过程，叫做解方程.也可以说，求方程的解集的过程叫做解⊃程.在不同的数集里解同一个方程，所得的解集不一定相同.例如方程

(x²+1)(x²-1)(x²-2)=0

在有理数集里有两个根是±1，其解集是{1,-1}；在

实数集里有四个根是

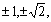
那么在实数集里

解此方程所得解集为

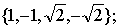
；在复

数集里解此方程则有六个根：

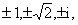
故得

解集为

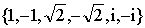
.再如方程

x²+1=0，在实数集里是矛盾方程，在复数集里则不是矛盾方程.一般地，应指明在什么范围（数域）里研究.中学数学里解方程时若不明确求解的范围（数域），即是指在实数域里求解.

方程Fangcheng

含有未知数的等式叫做方程。例如， 3x=6,x-10=4, y²+2=4y-1等都是方程。方程中所含的未知数， 叫做方程的 “元”。一个方程中含有几个未知数，就叫做几元方程。例如，x+3=5，叫做一元方程； x+y=5, 叫做二元方程， 等等。
方程可以由组成它的代数式的形式， 分为以下各类：
整式方程， 又可以由组成它的代数式中所含未知数的个数及各项中未知数的最高次数，分为以下各类：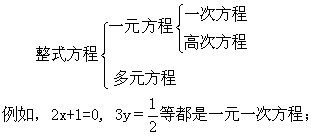
2x+3y=0.5xy+6=0分别是二元一次和二元二次方程。
又由于方程是含有未知数的等式，因而，方程又可以根据未知数的取值情况进行分类如下： 恒等方程——未知数可以取任意数值。例如， 5x+1=2x+1+3x。条件方程——未知数只可取应有的值。例如， 2x+1=0, x²-2x+1=0, x+y=0等。矛盾方程——未知数不可能取任何值，或在指定的数的范围内，没有适合于方程的未知数的值。例如，x²+1=2+x²以及在实数范围内的方程5x2+1=0等。

---

方程Fangcheng

做为现在通用的数学名词，方程指含有未知数的等式。但在中国古代，它最初的含义是线性方程组。《九章算术》（参见该条）有专门的“方程”章，方即方形，程即考核、表达， “方程”意为“方形的表达式”。中国古代在表示线性方程组时，《九章算术》 中的 “方程”未知数的记法并不出现，只写出其各项系数，在用算筹表示时，以纵向为行，各行自右至左排列，组成了一 个长方形的数字阵，因此称为“方程”。《九章算术》方程章第一题计算上、中、下三种稻子的产量， 相当于求解线性方程组：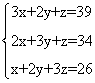
书中这一表达式的列法如上图。
在今天的意义下使用“方程” 一词，在中国始于清代后期，译自英文equation一词。equation的拉丁文为æquatio，原意为等式， 后来指含有未知数的等式， 但也可以指比例式。1859年，李善兰翻译英国数学家德·摩根(DeMorgen)《代数学原理》(1835)，将equation译为方程，1872年华蘅芳译《代数术》则称为方程式。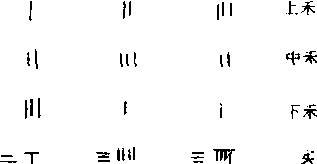
即使仅限于代数学范围， “方程”的含义也相当丰富，但在19世纪以前，代数学研究的主要是各种代数方程，包括它们的建立，表示和求解，占核心位置的是多项式方程。
涉及一元一次方程的问题很早就出现在巴比伦、埃及、中国、印度的古代数学中。在大多数场合，它主要是根据比例、配分比例的原理求解的，其中代数学的思想与方法并不明显。
巴比伦人很早就求解过许多线性方程组问题， 但其方法目前尚不知道。最早明确记载系统解法的是中国的《九章算术》，公元3世纪刘徽对其作了精彩的理论探讨， 同类工作在欧洲直到17世纪以后才陆续完成。
二次方程问题最初也是由巴比伦人在很早的时候就得到了求正根的 一般方法。在古希腊，二次方程求正根的公式首先以几何形式出现在欧几里得《几何原本》中，代数形式由1世纪的海伦(Heron) 明确给出。在中国， 《九章算术》中已明确载有二次方程，并已具备了求解的能力， 求正根的明确公式到3世纪由赵爽和刘徽给出。
高次方程解法沿着数值解（近似解）与公式解（根式解）两个方向发展。巴比伦人曾处理过一些特殊的三次方程。最早系统地研究三次方程问题的专著是7世纪初中国数学家王孝通的《缉古算经》。11世纪，贾宪创立了开一般高次方的增乘开方法， 并给出了二项式系数表 （贾宪三角形）及其构造方法。1247年， 秦九韶对一般高次方程的数值解法作了系统而完整的表述。在西方， 同类工作直到19世纪初才由鲁斐尼(Ruffini,P.，意大利，1804)和霍纳(Horner,W.G.，英国， 1819) 作出。
自希腊数学之后， 西方代数学中长期处于核心位置的问题是三次以上代数方程的根式解。其中，三次方程的一般求根公式于1541年由塔塔格利亚 （参见该条） 给出， 其后， 费拉里 (Ferrari. L.) 得出四次方程的一般求根公式，1545年，卡尔达诺（参见该条）将这两种解法发表在他的《大术》一书中。此后，寻求五次以上代数方程根式解的努力在19世纪终于导致了群论的诞生。
在代数学的内容主要以普通语言而不是以符号表述的时代，建立二、三次方程需要借助几何意义和高度的技巧，四次以上的方程的建立就更加困难。12世纪，中国数学家创立了 “天元术”，即设立未知数建立代数方程的一般方法，其原理与今天的方法完全一致。代表作是李冶的《测圆海镜》(1248)。在欧洲， 自由地建立高次方程直到16世纪中叶以后才实现。
在西方15世纪以前对代数方程的表述用普通语言，此后逐渐向符号代数演变，直到17世纪末才达到今天的记法。在中国，一元高次方程在宋元时代已有成熟的分离系数表示法，但在向多元高次方程发展时，由于所有未知项的系数仍用平面上的位置表示， 达到4个未知数的多元高次方程组的建立， 表示与消元法后便停止了发展。其中， 朱世杰在1303年的 《四元玉鉴》中系统地论述了上述方法，他给出的多元高次方程组消元法在欧洲直到1779年才由法国数学家贝祖(Bezout, E.) 正式发表。

方程

含有未知量的等式。使等式成立的未知量的值称为方程的解或根。求解的过程称为解方程。例如，x²+1=3-x是方程，它的根是1和-2。不论未知量的值如何，总是成立的等式称为恒等式。例如：(x-1)²＝x²-2x+1。

方程

equation