控制论在生理学中的应用

机体功能的调节和控制是生理学研究的中心课题之一。早在古希腊的时候，就有人设想，人体的健康是由机体的平衡所保证，而疾病是由于机体的不平衡所引起。许多世纪以来，生理学家们对机体功能系统调节和控制的研究，取得了大量的成果，有力地阐明了机体的功能。自从控制论诞生之后，控制论的基本思想几乎渗透到各个学科领域，尤其对生理学中控制和调节的研究更具有重大意义。它使生理学研究从定性过渡到定量，从静态过渡到动态，从而推动了生理学的研究不断向纵深发展。控制论的概念是1948年维纳提出的。维纳把控制论定义为关于在动物和机器中控制和通信的科学。控制论既是一种重大的科学理论，又是一种有力的方法论，因为它确认世界上的一切事物都以信息为媒介存在着普遍的联系； 它又试图提供探索这种普遍联系的方法。正因为这样，控制论的理论和概念就不是那些研究某一类客观现象的具体科学中的理论和概念，而是能够适用于一切对象的理论和概念。它涉及的内容很多，而且有些目前还不统一。下面介绍对生理学研究有重要意义的系统、信息和反馈这三个最基本的概念。
系统是由一定元件（或部分）组成的一个整体。系统概念中的这种整体并不等于各部分的简单总和，而是各部分之间的有机结合，从而表现出各个组成部分所不具有的那些特征。每一个系统，总是可以完成某种特定的功能。根据功能的不同，系统的规模可大可小，它既可适用于整个宇宙空间，也可适用于每个小的分子或原子，而且在一个系统中也可以包含另外一些子系统或分系统，这也就是说，系统是分层次或水平的。因此，控制论所研究的系统往往是那些在某个特定水平上“相对独立”的系统。所谓“相对独立”系统，必需具备两个特点：
❶是以特定的途径输入，来接受宇宙间其他事物的影响；
❷是以特定的途径输出，来对宇宙间其他事物施加影响。这种“相对独立”系统可用图1的框图来示意。

图1 系统框图

当然，对一个系统来说，它的输入和输出可以是一个，也可以是多个。控制论的任务，就是要对那些被研究的系统，根据其完成的功能，并按照“相对独立”系统的原则，预先对系统规定出一个明确的界限，然后把系统的各个组成部分暂定在一个特定层次或水平上，而不是对系统中的一切细节作全面的考察。只有这样才能真正把握住这个系统的本质。
信息从狭义来讲，就是关于系统外部或内部情况的消息。从广义来讲就是事物存在的方式和运动的状态。世界上一切事物都是在运动着，它们的运动状态给我们提供了各种各样的信息。控制论就是要从数学上定量研究系统中各种信息的传递、加工和控制的规律，以使整个系统工作处于最佳状态。如果一个系统没有信息进行流通，那么整个系统将无法工作。
反馈就是把系统的输出返回送到系统的输入，借以减少外界因素对系统输出的影响。当然反馈有正负之分。正反馈是输出强化输入，负反馈是输出控制输入，并调整过度行为，矫正最佳值的偏差(以后如不特别指明，“反馈”一词均指负反馈而言)。因此，反馈是一种调整输出使其接近平衡状态的方法，这种方法无论在自然界，工程技术上和生物机体中都是经常利用的，普遍存在的，凡是一个系统都是在反馈的基础上进行的。
控制论的诞生为生理学研究提供了新的研究思想和新的方法。在生理信息的测试与处理，机体功能的模型与模拟，以及在生理功能系统分析等方面，控制论的理论和方法是起着重要的作用。本条目着重叙述机体功能的模型与模拟和生理功能系统分析等部分。
生理功能系统的确定 从控制论的角度来说，所谓生理功能系统的确定，就是要探讨信息在生理功能系统中的传递、加工和控制，亦即信息的交换、加工和走向方式的选择等问题。
有机体是由若干功能系统组成的。每个系统又包括了许多结构和功能上各不相同的器官，各个器官又是由几种不同类型的组织所组成。因此在生理学的研究中可分为几个不同水平的系统：整体水平，器官水平及细胞或分子水平的功能系统。几种水平研究的对象和任务，既有联系又有区别。但是作为一种系统结构它们又是一致的。因此，可用一种统一的手段来加以处理。虽然各种系统的具体形式和内容不一样，但目的都是要使某一功能活动在某一特定点上保持相对稳定或达到某种规定的状态。具体情况如图2所示。

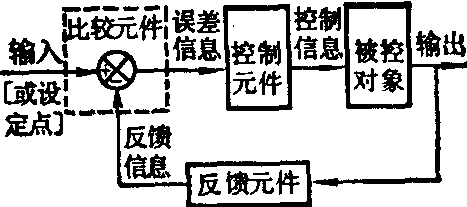
图2 一般生理功能系统结构图

图2的功能系统是一个反馈系统。在机体内这种反馈系统是大量的，十分重要的，是维持正常功能不可缺少的。凡是使某种功能在一定状态上保持相对稳定的生理功能系统都属于这一类。它包括如下几个基本要素： 被控对象，比较元件，反馈元件和控制元件。我们以血压调节系统为例来理解各要素的作用。正常人的动脉血压在一定水平上能保持相对恒定，就是因为它是一个反馈调节系统。如图3所示。

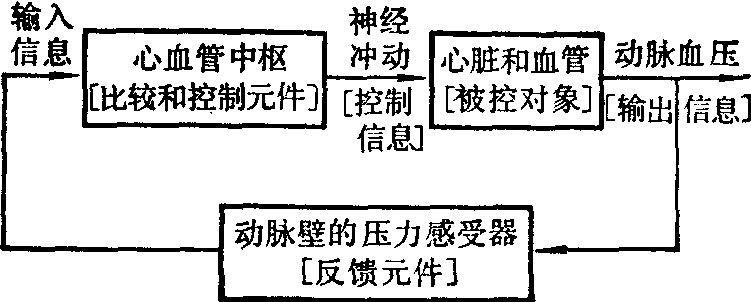
图3 动脉血压调节系统框图

如图所示，中枢神经系统内有心血管中枢 （相当于控制元件），它发出的控制信息以神经冲动形式传到心脏和血管（被控对象），动脉血压就是要求的输出信息，在动脉管壁上有压力感受器（反馈元件），它可感受动脉血压的变化，并发出反馈信息，通过传入神经送回心血管中枢（比较元件）。这里应该注意，有时比较元件和控制元件是由同一个器官或组织来完成的，本例就是这样，神经中枢既是控制元件又是比较元件。而在某些场合，它们往往是独立的，在对具体系统进行分析时这点要十分注意。上述表明，动脉血压之所以能经常保持恒定，神经中枢内可能有一个决定动脉血压大小 （设定点） 的机构，它能发出参考信息到心血管中枢。当某种扰动使动脉血压上升时，血管壁上的压力感受器受到的刺激增强，因而送回相应的反馈信息，此信息在神经中枢与设定点的参考信息进行比较，得出的误差信息被用来纠正心血管中枢的控制信息，使动脉血压降回到原来的水平。反之，当某种原因引起血压降低时，这套机构起相反的作用，使血压升回到原来的水平，维持血压恒定。总之，各种生理功能活动之所以能保持相对稳定，主要是由于负反馈信息的作用，而在什么状态上保持相对稳定，则取决于设定点的状态。在生理功能系统中相当于工程系统的设定点是存在的，如正常人的血压，血糖，体温等都有一个设定值，保持相对恒定。但设定点究竟是那一个机构来维持的，这些恒定值是怎么确定的，现代生理学中还没有肯定的结论，可能是在长期进化过程中确定下来的。尽管有关各个生理参数设定点的解剖位置以及设定值的确定，还有待生理学进一步深入研究，但是设定点学说的观点，已日益普遍地为人们所接受。
要实现系统的控制，首先是解决信息在系统中的流通问题，在生理功能系统中信息流通，主要是靠神经、体液和神经体液等形式来实现。
应该注意，当我们对生理功能系统各元件进行分析时，要按照系统“相对独立”的原则。因为在一个特定系统中，各元件本身也许就是一个非常复杂的子系统，它可能是由另外一些更小的元件构成的反馈系统； 但由于特定系统的机构已经确定，它是作为系统的一个元件而存在，因而就不应该对它进行更细的考察。但是，如果要具体了解该元件的信息加工能力时，对元件进行仔细分析乃是完全必要的。
根据系统和相对独立系统的概念和原则，生理功能系统与工程系统的功能和结构是一致的。因此，从控制论的角度来看，完全可以把生理功能系统作为系统来研究。但是我们都知道，在工程上是人们为了达到一定的目的而设计某一工程系统，而人体功能系统则是亿万年来长时间进化形成的结果。它与工程系统相反，不是人工设计出来的，而是通过研究一步一步地把业已存在的系统结构图发掘出来。故两个系统又有本质的差别，这是可以想象的。
两个系统的第一个差别，就是工程系统一般多为线性的。虽然控制论的早期工作一般都是研究线性系统，但近年来已发展到对非线性系统进行研究。而生理功能系统却不同，它几乎都是非线性的。对线性系统的活动用数学方法进行分析和预测时，所需要的资料比较完全。由于生理功能系统绝大多数为非线性的，因此在分析生理功能系统时有两种办法，一是用数字计算机直接模拟非线性的生理功能； 一是把复杂的非线性曲线中有用的部分人工地进行近似线性化处理，使要分析的部分线性化后再进行数学模拟和分析。我们以Grodins的呼吸生理中的CO₂解离曲线为例进行说明。图4的点线是实测曲线，可用如下的公式表示：
Ca=0.107(PaCO₂)^0.415
式中Ca是动脉血中的CO₂含量，PaCO₂表示动脉血中CO2分压。此式很明显是非线性的。如对点线的最后一部分进行近似线性化处理（图中实线），则上式可变为直线公式如下：

Ca=0.00425PaCO2+0.32

这样就可以在规定的范围内按线性系统进行分析处理了。

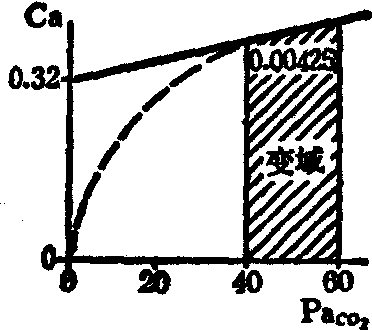
图4 线性化CO₂解离曲线

第二个差别是生理功能系统没有明确的基准输入（设定点）和偏差检出部分（比较元件），这从上面血压调节框图和一般生理功能系统结构框图中就可以看出。但从生理功能实际作用来看，确实存在这种功能，可设想其执行机构是存在的，并且是在长期进化过程中形成的，只不过在生理学研究中尚未被阐明而已。
第三个差别是工程系统中元件的输入、输出都比较明确，而且几乎都是一个输入和一个输出，适用于拉普拉斯(Laplace)变换；而生理功能系统中元件的输入和输出就不十分清楚，而且它们之间有几种对应，有的是几个输入对一个输出，有的是一个输入对几个输出，也有的几个输入对几个输出的混合形式，因此不能用简单的办法即知道输入输出就可以了解系统中元件的特性。为了避免这种困难，有两种办法，一是使输出只限于和输入有某一种函数关系，二是利用参数强制变更法。作为后者的例子有Grodins关于心脏活动的公式：

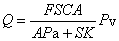
式中有三个参数，它们是心搏出量Q，静脉血压Pv，动脉血压Pa，其他符号均为常数(F是心收缩频率，S是心收缩强度，C是心室充盈度，K和A是有定义符号，K=e-[([⁰/^F)-0^.2]/^C, A=1-K,R是粘性阻力)。Q、Pv和Pa之间的关系可用框图表示如下：

图5 参数强制变更图解

图5表示对Pa进行强制参数变更的方法。
综上所述，生理功能系统和工程系统虽有一些区别，但经过处理完全可以用研究工程系统的理论、方法和先进技术工具对生理功能系统进行研究。它已经和将会促进生理学的深入研究，对进一步阐明生理功能系统的规律起重要作用。
生理功能系统数学模型的建立 数学模型就是要用数学的方法，对被研究的对象（系统或元件）提出一个信息加工模型，称之为数学模型。利用数学模型可以从数量上对系统进行分析，并研究其动态行为，因此可以认为数学模型是对系统或元件的输入输出关系所作的一种动态的、定量的描述。
在生理功能系统中，使用数学模型是从1948年控制论问世之后迅速开展起来的。数学模型的建立包括三个内容，模型的构型，模型的参数估算和模型的模拟。
模型的构型 传递函数是一种模型构型方式。它是当初始条件为零时，用微分方程描述对象的运动特征(即输入、输出关系)，然后再将输入输出进行拉普拉斯变换，从两者的比值求出传递函数。它能够表征任何一个元件或系统的基本特性，也即系统的输入输出之间的关系。设输入为X，输出为Y，则传递函数的一般表达形式为：

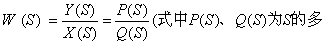
项式)，有了传递函数的概念之后，尽管研究的具体对象不同，但它们在数学上却可以用同一个式子来表达。例如，在电容、电阻的串联电路中，电容两端的电压变化规律，它和下文将要讨论的肺膜实验中肺膜内侧²⁴Na浓度的变化规律，就都可以用同一个传递函数K/_TS+1来描述。正是数学上的这种抽象性，给控制论的研究带来了极大的方便。人们只有学会撇开具体对象性质的特点之后，才能从更加抽象的高度来理解事物的本质。数学的产生和发展有力的证明了这一点。数学所重视的并不是具体事物本身，而是事物的普遍规律，控制论也是如此，它也不重视具体对象质的特征如何，而重视系统输入输出的关系即信息的传递加工和控制的能力。从控制论的观点来看，模型种类很多，对同一个对象可以提出不同的模型构型。其分类概括如图6。

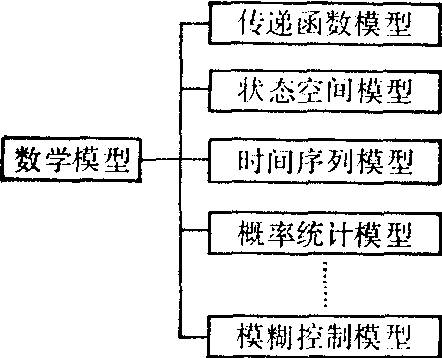
图6 数学模型构型分类

从图6可以看出，传递函数模型只是数学模型的一种构型方法，它是经典控制理论中经常用到的，但却是比较初级的。对生理功能系统的研究来说，由于生理学研究水平的限制，目前采用最多的还是这种方法。当然，随着生理学研究的不断发展，对生理功能系统建立更高级的数学模型不仅是可能的，而且是十分必要的。
模型的参数估算 这主要是求模型构型中的各项参数，以便使模型的输入输出关系符合生理学实验所获得的结果。为了找出模型的参数，常用的方法主要有三种：第一种方法是根据对象本身的物理化学过程以及已知的生理学知识，用解析的方法推导出来； 第二种方法是用标准输入信号 （阶跃或正弦信号） 对元件或系统进行测试，求出它的参数； 第三种方法是现代控制理论中常用的参数辨识法。在生理功能系统中，由于系统本身的非线性，而限制了第一种方法的应用，但在某些简化条件下，它仍然有一定的指导意义。目前常用的是第二种方法，或者是第一、二种方法的结合，而第三种方法在生理功能系统的研究中也已开始被应用，并显示出它的发展前途。
模型的模拟 就是将数学模型用工程的方法复现出来，以验证模型的结果是否可用。目前常用的方法也有三种： 模拟机模拟、数字机模拟和工程部件模拟。模拟机模拟是用积分、微分、放大、非线性函数等各种部件的相互联接来完成数学模型中的各种运算。它的优点是使用方便，但精度较差。工程模拟是用一些部件相互联接完成数学模型中的各种运算功能，如用液压部件模拟或用电子线路模拟都是工程模拟的方法。此法灵活性较差，很少应用。目前普遍应用的是数字机模拟方法，它有通用性、灵活性，因此它可以模拟生理功能系统的非线性特点，使用也很方便。
现在我们用一个最简单的例子来示范数学模型的建立、参数估算和模拟的整个过程。在肺膜实验中，可对²⁴Na通过肺膜的物理特性建立数学模型，如图7所示：

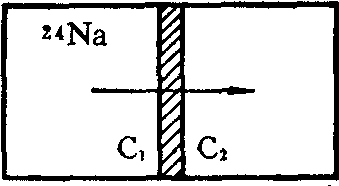
图7 ²⁴Na透过肺膜扩散图

C₁是肺膜外侧（即肺膜的循环侧）的²⁴Na的浓度，作为输入。C₂是肺膜内侧（即肺膜的肺泡侧）的²⁴Na的浓度，作为输出。它的运动用微分方程式可表示如下：

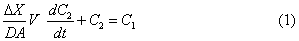
式中△X为肺膜厚度； A为肺膜面积；D为扩散系数；V为肺腔体积。(1)式可如下推出：


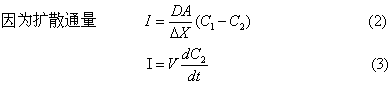
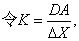
并将(2)代入(3)式加以整理可得：

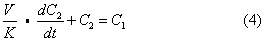
对(4)进行拉普拉斯变换并加以整理可得：

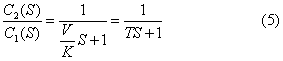
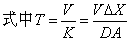
称为时间常数。

至此数学模型的构型已经完成，接着就是模型参数的估算，即求出时间常数T的数值，它可以从对象的物理参数直接求出，即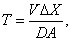这在简单的情况下是可以的，但在复杂的条件下是很难的，甚至是不可能的。这就需要用另一种方法，即用一个阶跃信号作为输入，让浓度C1作一个跳变，然后记下浓度C2的响应，结果如图8所示：
根据自动控制原理可知，C2(t)到达稳态值的63.2%的时间，便可认为是时间常数T，这样我们虽然不知道

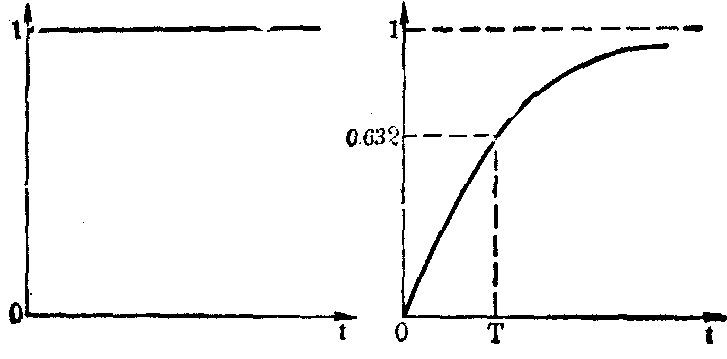
图8 时间常数T的测试结果

对象的具体物理参数(如△X、D、A等) 也可以估算出这个模型的参数。再下一步就是模型的模拟工作。为了模拟(5)式的传递函数，可以用简单的R、C线路来实现，也可以用模拟机的积分部件来实现(图9)。只要改变电阻电容的数值(T=RC)或改变积分器的反馈系数T就可以变更数学模型中的时间常数。当然(5)式的模型也可以在数字机上进行模拟。但是在这样简单的情况下就不必要了。

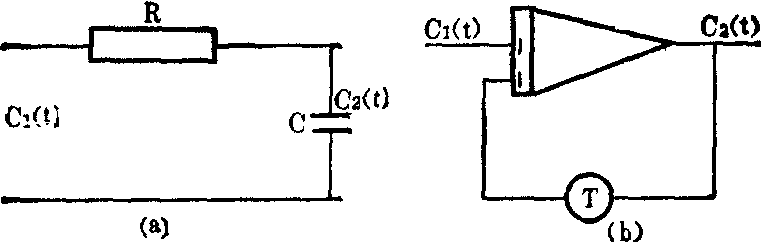
图9 传递函数的模拟

这是以最简单的例子来理解建立数学模型的过程。事实上在生理功能系统的研究中都是比较复杂的，因此我们再举一个比较复杂的血糖调节系统来试用上述方法，既能帮助进一步理解数学模型的建立和模拟，又能看到实际应用的作用。当血糖浓度升高时，过多的糖使胰脏的β细胞分泌胰岛素增加，胰岛素又可以使组织细胞对糖的透过性增大，因而糖进入组织内引起血糖下降。反之，当血糖降低时，胰岛素分泌减少，糖进入组织也减少，引起血糖增高，如此便形成一个胰岛素葡萄糖控制系统。其相互关系如图10所示。

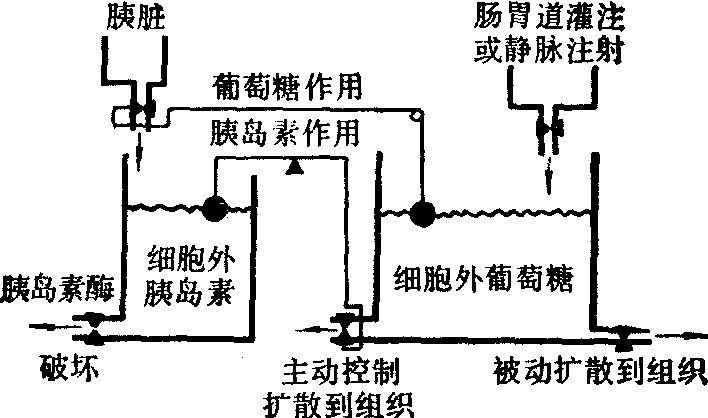
图10 胰岛素-葡萄糖控制系统原理图

根据以上的生理机理和物理化学过程的规律，可以写出描述葡萄糖浓度的方程式为：

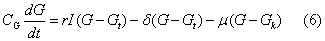
描述胰岛素含量的方程式为：

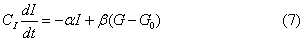
两个方程式的符号和单位以及常数和系数，都可以在一些特定的设想下，根据已有的生理实验数据进行推导标注出来。例如设想一个人体重是70kg，那么他的细胞外空间容积就相当于15L，由此可以推知葡萄糖的容量CG=150mg·mg%，胰岛素的容量CI=150mU·mU%。在很多情况下，细胞内葡萄糖量可以忽略，因为细胞内糖元很容易变成细胞外葡萄糖，因此可以设想有效的细胞内葡萄糖浓度G_t＝0。再举一个系数推导方法的例子，如求胰岛素的破坏系数α，根据胰岛素对胰岛素酶的反应，是一阶响应特点，可写成公式为：

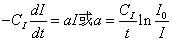
因为CI=150，又根据Drury的实验证明循环血流中的胰岛素有40%是被破坏。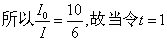时，则

α=150×0.506=76mU·h-¹·mU%-¹

表1 方程式中变量、符号、单位和数值的定义一览表

符号	定 义	单 位	数值
CG	细胞外空间的葡萄 糖容量	mg·mg%-1	150.0
G	细胞外空间的葡萄 糖浓度	mg%	—
Q	释放到细胞外空间 的基础葡萄糖	mg·h-1	8,400
r	胰岛素对葡萄糖利 用的影响系数	mg·h-1·mg%-1. mU%-1	13.9
I	细胞外空间的胰岛 素浓度	mU%	—
Gt	有效的细胞内葡萄 糖浓度	mg%	0.0
δ	胰岛素独立于葡萄 糖利用的系数	mg%·h-1·mg%	24.7
μ	葡萄糖在尿中的损 失系数	mg%·h-1·kg%-1	72.0
Gk	肾小管对葡萄糖重 吸收的最大值	mg%	250.0
CI	细胞外空间的胰岛 素容量	mU·mU%-1	150.0
α	胰岛素的破坏系数	mU·h-1·mU%-1	76.0
β	胰岛素的分泌系数	mU·h-1·mg%-1	14.3
G0	葡萄糖对胰岛素分 泌的阈值浓度	mg%	51.0
t	时间	h	—

用类似的方法，式(6)、(7)中的其他符号和系数也均可推导出来。由于这时已知的一些生理学数据是进行推导的基础，所以生理学的实验研究仍是十分重要的，它是研究生理功能系统必不可缺少的依据。各具体数据见表1。
将这些常数和系数代入方程式(6)、(7)则为：

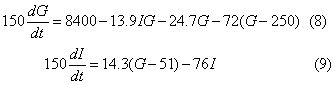
这两个方程可以用模拟机进行模拟，也可以用数字机进行模拟，甚至还可以用液压系统进行模拟。图11就是用这两个方程在数字机上进行模拟的结果。

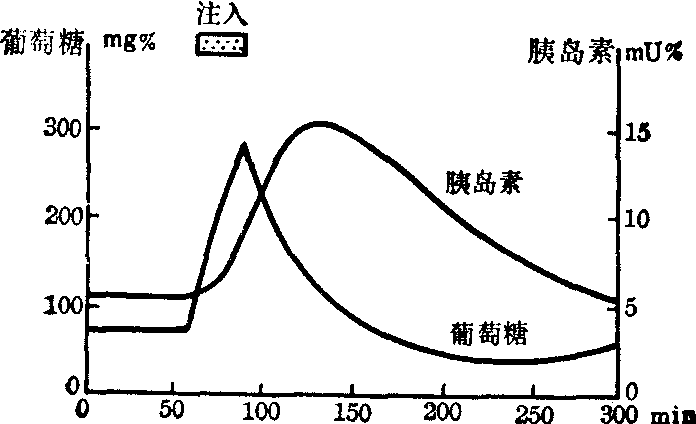
图11 灌注葡萄糖正常响应的模拟曲线(引自Mountcastle,1974)

通常，生理功能系统的各系统和元件的传递函数，可由一些典型的传递函数(比例、积分、微分、延迟、一阶滞后等)构成或是由它们组合构成。例如上述第一个例子就是一个一阶滞后元件，而胰岛素-葡萄糖控制系统是一个非线性比例积分的控制，在数字机上模拟需要求解一个二阶非线性方程。为了求得整个系统的传递函数，可先分别建立组成系统各元件的数学模型，其取得的方式如图12示意：

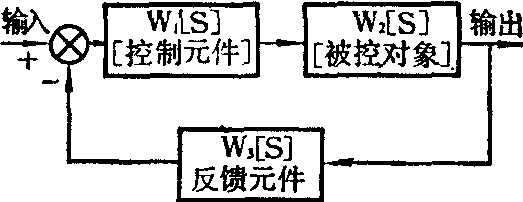
图12 系统传递函数求取框图

表达的方式如下：

生理功能系统分析 生理学研究的基本任务是阐明机体及各组成部分的生理功能、活动机理及内外环境变化对机体功能的影响，从而掌握和运用这些规律，进一步对疾病的发生发展过程和疾病的治疗等提供理论基础。控制论的方法是通过对生理功能系统的特点建立数学模型，再根据“黑箱”理论对机体生理功能进行系统分析。所谓“黑箱”理论，一般有四个要素需加以考察，即输入信息、输出信息、扰动信息和系统运动规律 （数学模型及其参数）。它们的关系如图13所示。

图13 黑箱示意图

根据四个要素的不同情况，可以对系统进行分析，解决不同问题，大致内容可归纳如表2:

表2 系统分析归纳表

类型		已知信息	欲得信息	解决的问题
Ⅰ	1	输入、输出、 无扰动	正常活动规律 （系统数学模型）	根据数学模型 分析生理机理
	2	输入、输出、 生理限度内的扰 动	生理限度内的 数学模型变化	确定生理限度 的范围
	3	输入、输出、 超生理限度的扰 动	超生理限度的 数学模型变化 （病态）	疾病起因的解 释
Ⅱ	1	输入、无扰动、 正常活动模型	输出	响应输出的预 报
	2	输入、生理限 度内扰动、生理 限度模型	输出	生理限度范围 的预测
	3	输入、超生理 限度扰动、超生 理限度模型	输出	疾病的诊断

从表2可以看出，利用系统理论深入研究生理机理，把有关理论应用到环境医学和环境生理学的研究中去，进行科学预测，以减少实验次数，并代替做环境因素对人体耐力界限的实验时，避免人体实验的危险，也可以在临床诊断上进行定量的、自动快速分析，提高临床诊断质量。
以脑缺血性全身动脉血压响应的稳定性的生理特性为例，来说明系统理论的应用。生理实验已经证明，脑缺血可以引起代偿性的全身血压升高。那么脑缺血到什么程度这种反应就减退或消失，在人身上做这样实验是难以实现的。但应用系统理论，可以用输入输出的响应关系的计算，预测其结果。现以三种不同程度扰动 (脑灌流压为60mmHg、40mmHg、30mmHg)的作用下，给予不同频率的正弦波的输入信息，测量动脉血压响应为输出，然后按照频率响应分析方法做出Ny-quist线图，即频率响应幅值比和相移极坐标曲线。当测出的曲线通过-1点或者包围-1点时，则表示血压调节系统达到不稳定状态，引起系统振荡。由图14可以看到，随着脑灌流压的降低，系统的稳定性随之变小，直至30mmHg时，系统发生振荡，说明系统调节功能失控。

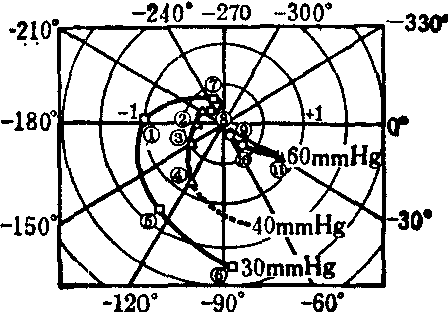
图14 三种不同情况脑缺血反应的Nyquist图

1. 1/49 2. 1/30 3. 1/49 4. 1/79 5. 1/79 6. f=1/126 7. 1/30 8. 1/20 9. 1/49 10. 1/7911. f=1/126

根据这种方法，我们可以方便地判断其结果。
自从控制论发表之后，在各门学科领域中均起到很大的影响。把控制论的理论和方法引进到生理学的研究中去，对生理学的发展也起到了重大的作用。