排序不等式paixu budengshi

证明不等式的一种方法.设有两个实数数列
(A)　a₁,a₂，…，a_n
(B)　b₁,b₂，…，b_n
任意给出数列(B)的一个重排

(B′) b_j¹,b_j²，…，b_jⁿ

把(A),(B′)逐项地对应相乘再求和得到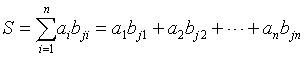

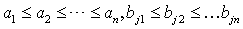当数列(A)和(B′)有相同的大小顺序时，称它们为同序；(A)和(B′)有相反的大小顺序时，称为逆序.即时为同序，

a1≤a2≤

…≤an,

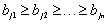，而时为逆序.当(A),(B′)同序时，S取得最大值；(A),(B′)逆序时，S取得最小值.用这一方法证明不等式就叫做排序不等式法.
固定数列(A),(B′)中各项不变，只交换(B′)中某两项b_jl和b_j^k，得到(B″).令S₁为(A),(B′)对应项乘积的和，S₂为(A),(B″)对应项乘积的和，如果a₁≤a₂≤…≤a_n，而b_j^lj^k，则容易证明S₁>S₂.不断重复这一过程，可以证明同序的和S最大，而逆序的和S最小.
应用排序不等式可以证明许多著名不等式而且比通常的证明方法简单.例如平均值不等式，柯西不等式，契比雪夫不等式等都可以用排序不等式给出证明.1978年全国数学竞赛试题中排队提水问题，1983年北京初三数学竞赛试题中给定两边取点搭配三角形面积问题，前者是逆序最小，后者是同序最大.这说明数学竞赛中常有以排序不等式为背景的问题.