招差术

080 招差术

古代用于天文历算和高阶等差级数求和的一种计算方法。属现代数学的有限差分法。它的发展与天文学的发展紧密相关。东汉刘洪在《乾象历》中推算定朔、定望的时刻所用公式为f(n+s)=f(n)+s_△，其中n为月球在近日点之后的整日数，f(n)为月球n日共行度数，△为一阶差分f(n+1)-f(n),0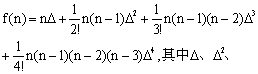
△³、△⁴分别表示各级差分的第一个差分。他指出公式中各项系数恰依次是“古法七乘方图”(贾宪三角的推广)中从左边开始的各斜线上数字的和。因此可以认为朱世杰已经掌握了任意高次的招差术。中国的二次内插法早于格雷果里(J.Gregory,1638-1675)1千多年，高次招差术也早于牛顿(I.Newton,1642-1727)近400年，是中国古代数学的一项杰出成就。参见32058二次内插法、32070平立定三差法。