投入产出分析
利用计量经济学分析并解决国民经济各部门之间经济联系并使其达到相互平衡的方法。这种方法是美国经济学家列昂惕夫于本世纪30年代首创。第二次世界大战后,随着电子计算机的广泛应用,投入产出的分析方法在西方比较普遍地推广。这种分析方法表明:国民经济各个部门在生产产品(即产出)的同时,又都在不断消耗各种物质资料(即投入),将这种投入、产出的数据按纵向与横向列成矩阵式的表格,就可以明确地表现出国民经济的某一个部门投入总量与产出总量之间的比例关系,并取得二者达到平衡所需要的条件。从这种比例关系,即技术系数中,可以求出某个生产部门的投入、产出的有关参数值。
投入产出分析
见“国民经济管理”部分“投入产出分析”。
投入产出分析
又称“消耗一产值分析”、“入量一出量分析”。通过编制投入产出表和经济数学模型(即反映经济系统各部分间数量联系的线性方程组),并借助电子计算机对国民经济各部分或部门内部各个环节之间的相互依存、相互制约关系进行分析和计划预测的一种方法。是一种主栏、宾栏都按相同部门分组编制的棋盘式平衡表。表内纵列反映某一部在生产消费过程中从其他部门得到的产品和劳务,即投入;表内横行反映某一部门的产品和劳务在其他部门的分配去向,即产出。根据投入产出表可以计算投入系数(也叫技术系数)和编制投入产出系数表,并利用数学方法从数量上分析部门间的经济关系和进行计划预测。
投入产出分析
[参]投入产出法
投入产出分析input-output analysis
20世纪40年代由俄国出生的美国经济学家里昂惕夫(W.Leontiel)提出的,用以分析和测度国民经济中各生产和消费部门之间联系的经济分析方法。这种方法的前提假设是生产技术不变且为线性,所运用的方法是一般均衡模型,目的在于对各部门经济活动的数量关系进行数值研究。现在,这种方法不仅广泛用于一个城市、一个地区或一个企业这样的经济系统,而且还应用于分析国际经济关系。投入产出方法假定每个部门生产一种同质产品(真实的同质产品或折算的同质产品),然后用一组线性方程表征各个部门的经济活动之间的数量依存关系。所以,系统的结构特征就取决于这些方程中的系数的量值。所以,应用投入产出方法时就要求有比较完整的基本统计数据。投入产出方法的典型应用有需求、产出、就业、投资等方面的影响等等。在投入产出分析中,如果假定劳动力投入所得到的产出是要经过一段时间的,这样得到的模型称为点投入点产出模型。
投入产出分析Input-output Analysis
广义是指投入产出法,即在一定的经济理论指导下,应用高等数学和电子计算机,研究各部门、各地区、各企业内部和它们之间的经济技术联系,进行各种经济分析、经济预测和政策评价的一种经济数学方法。狭义是指利用投入产出表,即根据国民经济各部门生产中的投入来源和使用去向而编制的矩阵形式的平衡表所作的各种经济分析。如分析国民经济各部门的直接、间接联系,主要比例关系、各种经济效益等。
投入产出分析
利用投入产出表和相应的投入产出数学模型所进行的经济分析。参见“投入产出表”。
投入产出分析touru chanchu fenxiinput-output analysis
经济计量学领域里研究国民经济各部门投入与产出的相互依存关系、产品的价值构成以及收入分配的一种综合平衡分析方法。亦称投入产出技术或部门联系平衡法。它是制定经济计划和进行经济控制的有力工具。
投入产出分析是美国经济学家瓦西里·列昂惕夫(W. W. Leontief)从20世纪30年代到50年代不断研究的结果。1936年8月,列昂惕夫在《经济和统计评论》上发表了题为“美国经济体系中的定量的投入产出关系”的论文,提出要注意经济体系的结构,注意一种经济的组成部分之间的组合方式和彼此的影响。他在论文中提出一个适用于任何发展阶段的任何一种经济体系的分析模型,即投入产出表。这种投入产出表明确地显示出每个经济部门对其他经济部门的依存关系,说明一种产业的产品怎样在其他产业和经济部门内进行分配,以及其他产业和部门怎样对该种产业进行投入。美国西弗吉尼亚州大学地区研究院院长、经济学教授威廉.H.密尔涅克称列昂惕夫的文章是“在不断革命的经济分析领域中掀起了一场默默的革命”。投入产出分析在不断发展中已成为计量经济学的一个重要分支。第二次世界大战期间在美国得到试用。世界上有100多个国家和地区推广使用这种分析方法。中国在运用投入产出分析上取得丰硕成果,国家、地区和部门的大型投入产出表已进入实用阶段。
投入产出分析的理论基础是经济发展均衡论,即国民经济各部门之间的依存关系在数量上应是均衡的。其研究方法是数理统计和线性代数。其主要内容是棋盘式的经济体系投入产出关系表和线性方程式体系两个部分。首先,根据国民经济的实际统计资料,按纵向为投入(又称消耗来源)和横向为产出(又称产品去向)的关系,将统计数据列入投入产出表。然后,列出数学模型,即线性方程组,通过矩阵运算,对统计资料进行加工处理,计算出各部门之间的直接消耗系数和完全消耗系数。在系数不变的情况下,利用这些系数和预定某些产品的社会最终需要量,计算出这些产品的中间消耗和总产量,从而进行国民经济计划平衡和计划测算工作。
在研究一个国家或一个地区的经济结构及其在发展中产业的比例关系,以及计划工作中的综合平衡等时,投入产出分析都是一种有用的经济数学方法。运用投入产出分析,可以检查现有计划的不平衡状况,分析国民经济的综合比例,编制合理的经济计划,研究采取某一项重要经济政策时可能产生的影响,为正确地确定产品价格提供科学方法和实际数据,以及进行经济预测等。
电子计算机的发展和运用为投入产出分析的数学建模和分析计算提供了极大的便利,从而为该方法的推广应用创造了更好的技术基础。
投入产出分析
利用计量经济学分析并解决国民经济各部门之间经济联系并使其达到相互平衡的方法。这种方法是美国经济学家列昂节夫(W·Leontief,1906— )于本世纪30年代首创。第二次世界大战后,随着电子计算机的广泛应用,投入产出的分析方法比较普遍地在西方推广。这种分析方法指出:国民经济各个部门在生产产品(即产出)的同时,又都在不断消耗各种物质资料(即投入),将这种投入、产出的数据按纵向与横向列成矩阵式的表格,就可以明确地表现出国民经济的某一个部门投入总量与产出总量之间的比例关系,并可以取得二者达到平衡所需要的条件,从这种比例关系,即其技术系数中,可以求出某个生产部门的投入、产出的有关参数值。联合国统计局于60年代末正式规定为有关国家国民经济核算的重要部分。但也有的国内外经济学家认为所谓“一般均衡”或绝对地平衡在西方资本主义社会或其他国家国民经济中都是不可能的,因而对这种方法的预测价值表示怀疑。
投入产出分析Input-Output Analysis
投入产出分析是研究经济系统各个组成部分间表现为投入与产出的相互依存关系的数量经济分析方法。美国经济学家瓦西里·里昂惕夫 (Wassily Leontief) 在前人关于经济活动的相互依存性的研究基础上,于1931年开始研究投入产出分析。他于1932年开始编制美国第一张投入产出表,分析美国的经济结构与经济均衡问题,并于1936年发表了题为《美国经济制度中投入产出数量关系》 的第一篇有关投入产出分析论文。1953年,里昂惕夫与他人合作,出版了 《美国经济结构研究》一书,首次系统阐述了投入产出分析的基本原理及其发展。由于里昂惕夫是投入产出分析的创始人及其对投入产出分析研究的巨大贡献,在1973年被授予诺贝尔经济学奖。
投入产出分析的思想渊源,最早可以追溯到18世纪法国重农学派魁奈的 《经济表》。但是,里昂惕夫研究和提出投入产出分析时所受到的直接启发,主要是19世纪下半期数理经济学派里昂·瓦尔拉提出的全部均衡理论及其数学模型。里昂惕夫在其著作中多次声称,投入产出分析是“全部相互依存 (general interdependent) 这一古典经济理论的具体延伸”(里昂惕夫,1980),是“用新古典学派的一般均衡理论对各种错综复杂的经济活动之间在数量上相互依赖关系进行经验研究” (参见涅姆钦诺夫,1980)。另外,里昂惕夫早年参与前苏联中央统计局编制国民经济平衡表的经验,对投入产出分析的创立也有不容忽视的影响。
投人产出表
| 产出 投入 | 中间需要 | 最终需要 | 总产出 | ||||
| 1 | 2 | … | n | ||||
| 中 间 投 入 | 1 | X11 | X12 | … | X1n | Y1 | X1 |
| 2 | X21 | X22 | … | X2n | Y2 | X2 | |
| … | … | … | … | … | … | … | |
| n | Xn1 | Xn2 | … | Xnn | Yn | Xn | |
| 附加价值 | N1 | N2 | … | Nn | |||
| 总投入 | X1 | X2 | … | Xn | |||
投入产出分析以投入产出表为基础。一般假设所分析的经济系统分为n个部门,如钢铁业、汽车业、电力事业、商业服务业等,分别用序号1,2,…,n代表。表中,Xij(i,j=1,2,…,n) 表示为生产j部门的产品所投入的i部门产品的数量; Yi (i=1,2,…,n)表示i部门产品中用于最终需用 (如消费、投资、出口等) 的数量; Nj (j =1,2,…,n)表示j部门产值中的附加价值; Xj表示j部门的总产值。
这是一张棋盘式的平衡表,是系统化了的投入产出分析的基础数据。把以上投入产出表横行或纵列的数值分别相加,可得到以下两组基本的方程式:
Xi1+Xi2+…+Xin+Yi=Xi(i=1,2,…,n)
(1)
Xij+X2j+…+Xnj+Nj=Xj(j=1,2,…,n)
(2)
令:aij=Xij/Xj,A= {aij}n×n,X= (X1,X2,…,Xn)T,Y= (Y1,Y2,…,Yn)T,并用I代表n阶单位矩阵,于是方程组 (1) 可表示为
(I-A) Y=X
(3)
当A的各元素aij<1时,(I-A) 的逆矩阵存在,且(I-A)-1=1+A+A2+A3+…
用 (I-A)-1左乘 (3) 式的两端,则得
X= (I-A)-1Y
(4)
(3)和 (4)通常被称为投入产出行模型(Input-output Model According to Row)。它揭示了总产品X和最终产品Y之间的数量依存关系。只要给定了最终产品 (或总产品)就可以求出总产品 (或最终产品)。
再用Âc代表各部门物质消耗系数对角矩阵,N为各部门附加价值向量,即
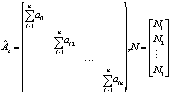
于是,方程组 (2) 可表示为
(I-Âc) X=N
(5)
再用 (I-Âc) 的逆矩阵左乘 (5) 式两端,可得
X= (I-Âc)-1N
(6)
(5) 和 (6) 式通常被称为投入产出列模型 (Input-output Model According to Column)。它描述了总投入X和附加价值N之间的数量关系。只要给定了附加价值 (或总投入)就可以测算出总投入 (或附加价值)。
里昂惕夫还建立了动态投入产出模型(Dynamic Input -Output Model),旨在引入投资时滞,以反映不同时期的部门联系,求得动态经济平衡。这种模型的关键是使投资内生化。这要把最终产品Y划分为投资I和最终净产品S两部分。平衡关系式为
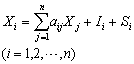
引入资本系数矩阵 (又称投资系数矩阵)B= {bij}n×n,bij=Iij/ΔXj,其中bij表示j部门每增加单位产量所需i部门投资产品的数量。加上时间下标t后,动态投入产出模型可用矩阵向量表示为:
(I-A+B) Xt=BXt+l+St
(7)
上述动态模型包含许多严格假定,如各部门没闲置生产能力,投资时滞为一年等。里昂惕夫于1970年发表 《动态逆阵》 一文,阐述了这种模型的求解问题。
投入产出分析作为一种经济数量分析方法,注意到中间产品 “迂回生产”所形成的周转在一国经济发展中的重要性; 清晰地反映出各部门之间的生产联系; 有利于分析特定系统内任何经济变动所引起的一系列波及效应; 为对整个经济活动进行统计描述收集和积累资料提供了方便,并且具有模型简单、意义明确、易于掌握和运用等优点。
但是,投入产出分析也存在着固有的缺点,如: 把生产函数只看作是线性的,不能反映现实经济中各投入要素之间,以及投入与产出之间复杂的数量关系; 没有考虑到最终需求的确定也会受到生产和收入的反馈影响;把所有数量关系都看成是确定性的,不注意随机问题; 没有真正解决技术变化、固定资本和耐用消费品的周转以及生产和收入中的时间差距等一系列动态问题等。
尽管如此,投入产出分析诞生以来不断地受到经济学界和各国政府的重视,其应用范围也不断得到扩展。它除了用于国民经济结构分析、价格形成和价格波动分析、经济政策模拟和经济预测之外,还可用于企业和地区的经济分析、地区间以及国际间的经济合作与贸易关系分析,用于环境保护、水资源合理使用、能源合理消耗、以及人口和教育投入产出分析等等。特别是随着投入产出方法和经济计量学、数学规划法、最优控制理论等其他经济数学方法的结合使用,以及经济信息化和编表技术的日益发展,投入产出分析必将越来越受到人们的重视。
投入产出分析
投入是指生产过程中消耗劳动对象、劳动资料和活劳动的数量,产出是指产品分配使用的方向和数量。投入产出分析是基于经验的数据,对一个社会、部门或企业内部的相互依存关系,进行全面分析和预测的一种科学定量分析方法,1936年由美国经济学家列昂节夫首次提出,它的基本内容包括理论基础、平衡表和数学模型三个方面,它把这种相互依存的关系用产品消耗的投入产出表反映。投入产出分析是建立在对部门产品流向分析基础上的,它的目的在于求出要满足消费、投资和出口的最终需求,各部门必须增加的实际产量,即应包括最终需求和各生产部门的中间需求两部分。
投入产出分析
经济计量学关于社会经济体系中各部门消耗工料数量 (投入) 和生产产品数量(产出)的相互依存关系,产品的价值构成、以及收入分配的综合平衡的分析方法,是一种系统分析的方法。它是美国经济学家里昂惕夫(W·W·Leontief)在本世纪30年代到50年代不断研究的成果,当前已被各国广泛采用。投入——产出分析主要通过棋盘式经济体系 (如投入产出平衡表) 和线性方程式体系两个部分进行。
投入产出分析input-output analysis
20世纪40年代由俄国出生的美国经济学家里昂惕夫(W.Leontief)提出的,用以分析和测度国民经济中各生产和消费部门之间的联系的经济分析方法。这种方法在生产技术不变的线性化假设之下,利用一般均衡模型对各部门经济活动之间的数量关系进行数值研究。现在,这种方法既广泛用于一个城市、一个地区或一个企业这样的经济系统,也用于分析国际经济关系。
投入产出方法假定每个部门生产一种同质产品(真实的同质产品或折算的同质产品),然后用一组线性方程表征各个部门经济活动之间的数量依存关系。所以,系统的结构特征就取决于这些方程中的系数的量值。应用投入产出方法,要求有比较完整的基本统计数据。投入产出方法的典型应用,包括需求、产出、就业、投资等方面的预测,分析工资、利润率、税制的变化对价格的影响和对整个经济系统的影响;研究自然资源利用,制定发展计划和分析国际间或地区间的经济关系等。
世界上大部分国家都已经在不同程度上采用投入产出分析方法。
- laborious是什么意思
- labot labat是什么意思
- labo(u)r是什么意思
- labour是什么意思
- labour day是什么意思
- laboured是什么意思
- labourer是什么意思
- labour force是什么意思
- labouring是什么意思
- labour party是什么意思
- labour party 工党是什么意思
- labour relations是什么意思
- laboursome是什么意思
- labour theory of value是什么意思
- labour union是什么意思
- la boétie etienne de 拉博埃西是什么意思
- labra是什么意思
- labrador是什么意思
- labrador current是什么意思
- labrador 拉布拉多是什么意思
- labrang是什么意思
- labras是什么意思
- labrau是什么意思
- labri是什么意思
- labri hpun是什么意思
- labri labra是什么意思
- labri lap是什么意思
- labri si是什么意思
- la bruyere,jean de是什么意思
- la bruyère jean de 拉布吕耶尔是什么意思
- labu是什么意思
- labuan是什么意思
- labuk是什么意思
- labuk labak是什么意思
- labu lago是什么意思
- labu matu是什么意思
- laburnum是什么意思
- labye是什么意思
- labying是什么意思
- labyrinth是什么意思
- labyrinthe 迷宫是什么意思
- labyrinth fish是什么意思
- labé louise 拉贝是什么意思
- lac是什么意思
- lacan jacques 拉康是什么意思
- lacca是什么意思
- laccadive,minicoy,and amindivi islands是什么意思
- lace是什么意思
- laced是什么意思
- la ceiba是什么意思
- lacewing是什么意思
- laches是什么意思
- lachesis是什么意思
- lachlan river是什么意思
- lachrymator是什么意思
- lachrymose是什么意思
- lachyang lap是什么意思
- lachyem是什么意思
- lachyen lahka是什么意思
- lachyit是什么意思