托宾回归
托宾回归Tobin regression
潜在变量yi*由下式给出:
yi*=β′xi+εi
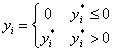
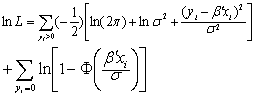
该函数相当复杂,但用Olsen(1978)的重新参数化表示可以获得很大的简化,令γ=β/σ,θ=1/σ。则对数似然函数化为:
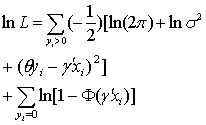
除了它非常简单的结构外,这种形式还有海赛(Hessian)矩阵总是负定的优点。这样,牛顿法易于使用,且通常收敛迅速。收敛后,原始参数可用β=γ/θ,σ=1/θ来恢复,这个估计量的渐近协方差矩阵可以利用下式从γ,θ的估计量的渐近协方差矩阵得到:
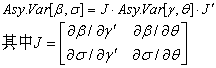
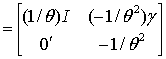
☚ 断尾回归 非均衡模型 ☛
- 俄罗斯水体建设工程限制立法是什么意思
- 俄罗斯水体开发利用目的立法是什么意思
- 俄罗斯水体影响工程限制立法是什么意思
- 俄罗斯水体恢复保护费立法是什么意思
- 俄罗斯水体所有制形式立法是什么意思
- 俄罗斯水体损失赔偿立法是什么意思
- 俄罗斯水体放射物质防污立法是什么意思
- 俄罗斯水体有害作用标准立法是什么意思
- 俄罗斯水体污染违法处罚立法是什么意思
- 俄罗斯水体污染防治立法是什么意思
- 俄罗斯水体泄污场所立法是什么意思
- 俄罗斯水体渔业开发立法是什么意思
- 俄罗斯水体游乐开发立法是什么意思
- 俄罗斯水体电力开发立法是什么意思
- 俄罗斯水体禁止垄断立法是什么意思
- 俄罗斯水体管理权力立法是什么意思
- 俄罗斯水体联邦所有制立法是什么意思
- 俄罗斯水体航运开发立法是什么意思
- 俄罗斯水体许可证制度立法是什么意思
- 俄罗斯水体防污保护立法是什么意思
- 俄罗斯水体限用立法是什么意思
- 俄罗斯水使用权许可证立法是什么意思
- 俄罗斯水关系主体立法是什么意思
- 俄罗斯水关系范围立法是什么意思
- 俄罗斯水利平衡立法是什么意思
- 俄罗斯水法定义立法是什么意思
- 俄罗斯水法律体系立法是什么意思
- 俄罗斯水法律目标立法是什么意思
- 俄罗斯水源保护区使用立法是什么意思
- 俄罗斯水源保护区建立立法是什么意思
- 俄罗斯水源保护区林地立法是什么意思
- 俄罗斯水资源保护立法是什么意思
- 俄罗斯水资源规划立法是什么意思
- 俄罗斯水违法处罚立法是什么意思
- 俄罗斯注册非法土地契约处罚立法是什么意思
- 俄罗斯洪涝灾害预防立法是什么意思
- 俄罗斯海洋环境污染违法处罚立法是什么意思
- 俄罗斯特护水体立法是什么意思
- 俄罗斯特殊用水立法是什么意思
- 俄罗斯环境保护立法是什么意思
- 俄罗斯环境保护许可立法是什么意思
- 俄罗斯生态放水要求立法是什么意思
- 俄罗斯生态物质违法处罚立法是什么意思
- 俄罗斯生态监测系统立法是什么意思
- 俄罗斯生态鉴定原则立法是什么意思
- 俄罗斯生物安全违法处罚立法是什么意思
- 俄罗斯用水付费原则立法是什么意思
- 俄罗斯用水付费征收立法是什么意思
- 俄罗斯用水许可证内容立法是什么意思
- 俄罗斯用水许可证收费立法是什么意思
- 俄罗斯用水许可证立法是什么意思
- 俄罗斯用水许可证终止立法是什么意思
- 俄罗斯用水许可证调整立法是什么意思
- 俄罗斯用水限额立法是什么意思
- 俄罗斯自然保护区资源保护立法是什么意思
- 俄罗斯自然保护目标立法是什么意思
- 俄罗斯自然保护立法是什么意思
- 俄罗斯自然科学保护区保护立法是什么意思
- 俄罗斯边区土地资金使用立法是什么意思
- 俄罗斯边区土地资金制度立法是什么意思