微分wēi fēn

稍稍看清。杜甫《奉赠太常张卿》：谬知终画虎，微分是醯鸡。

微分←→积分wēi fēn ← → jī fēn

微分：描述物体运动的局部性质的学科。如求运动着的物体在某一瞬间的运动速度就是微分学的问题。
积分：描述物体运动的整体性质的学科。如由运动物体在各点的瞬间运动速度求物体运动的全部路程就是积分学的问题。
【例】 这一时期最重要的成就是出现了解析几何和微积分，它们是近代数学的基础。(吴义生等： 《自然科学概要》)

微分weifen

是微积分的重要概念之一。设函数y=f (x)在点x₀的某个邻域内有定义。若函数y=f(x) 在点x₀的改变量Δy可以表示为

Δy =AΔx +o(Δx),　(1)

其中A与Δx无关而与x₀有关，则称函数f (x)在点x₀可微，ΔAx称为函数f (x)在点x₀的微分，记作dy |_x=x0＝ AΔx。
微分具有以下两个特点：
❶ dy=AΔx是Δx的线性函数，表达式简单。

❷ Δy-dy=o (Δx)，即Δy与dy相差一个比Δx高阶的无穷小量。换言之，用微分代替改变量，当|Δx|充分小时，不仅误差|Δy-dy|本身很小，更重要的是，其相对误差|(Δy-dy)/AΔx|可以任意小。所以，在式(1)右端，AΔx起主要作用。
上述的两个特点表明，微分dy是Δy的既简单而又具有一定精确度的近似表达式。
函数f(x)在点x₀可微的充分必要条件是f(x)在点x₀可导，且 (1) 中的A等于f′ (x₀)。
这表明，一元函数的可导与可微是等价的。函数y=f (x)在点x₀的微分可表示为dy|x=x₀＝ f′ (x₀) Δx。
若函数y=f (x)在区间I上的每一点都可微，则称f (x)为I上的可微函数。函数y=f (x)在区间I上的微分记作dy=f′ (x)Δx。d y既依赖于x，又依赖于Δx，而x与Δx是互相独立的两个变量。
通常约定，自变量x的微分dy=Δx。于是，

d y =f′ (x)dx,

从而有　。
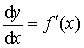记号dy/dx具有双重意义。作为整体记号，它表示f (x)的导数f′ (x)；作为运算记号，它表示函数的微分与自变量微分之比。因此，导数也称为微商。

微分

函数y=f(x)的自变量有一改变量△x，那么函数值对应的改变量△y的近似值f′(x)△x称为y的微分，记为dy=f′(x)dx。f′(x)是f(x)在x点的导数。对多元函数，如二元函数u=f(x,y)，若对x和y的偏导数都存在，称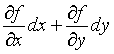是u在(x,y)点的全微分。记为du。

微分differentiation

确定一个函数的导数的过程；又叫求导数。
导数的概念与边际的概念很接近。边际概念可定义为与自变量的一个单位相关的因变量的变化。通过一个函数y=f(x)中变化的特性更精确地说明这一关系，用△x表示自变量x值的变化，用△y表示因变量y值的变化，△y/△x的比值最概括地反映了上述边际概念。
求导数就是在自变量极小的场合下求△y/△x的比值。导数的数学符号是：

其读法是“当△x接近零时，y对x的导数等于△y/△x比值的极限。”
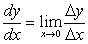
导数作为比值极限的概念恰好等于曲线上某一点的斜率。附图示出这个概念。

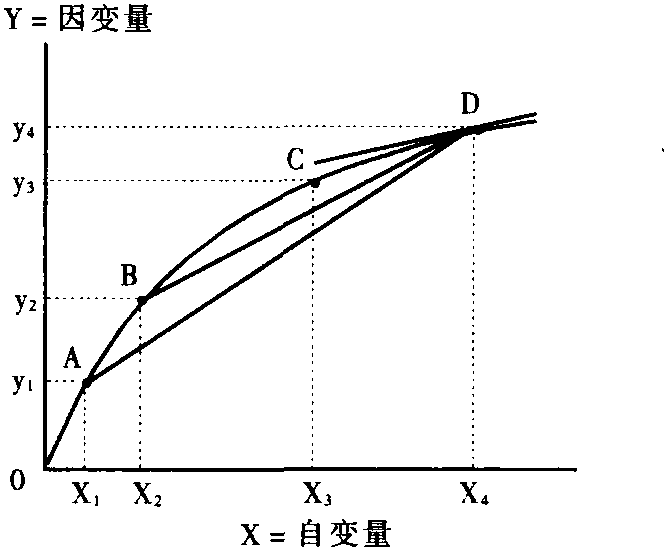
导数作为曲线斜率的示意图

图中的曲线在A点与D点之间的平均斜率测定如下：

这个平均斜率表现为连接两点的弦的斜率。同样，它可在x值的更小的区间加以测定，并用其他弦来表示。在到达极限时，即当△x接近零时，△y/△x比值等于在曲线的D点上所作切线的斜率。这条切线的斜率定义为函数在D点的导数dy/dx，它测定与x值的一个很小的变化相联系的y值的边际变化。
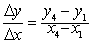
微分是一种很好的分析方法，它通过边际分析可用来确定目标函数的最大值与最小值，提供管理经济学方面的有用信息，特别易于推广应用于解决管理决策中约束最佳化的问题。确定一个函数的导数只要对函数应用一个基本公式就行，它在微积分教程中可以找到。