平面曲线的弧长
平面曲线的弧长pingmian quxian de huchang
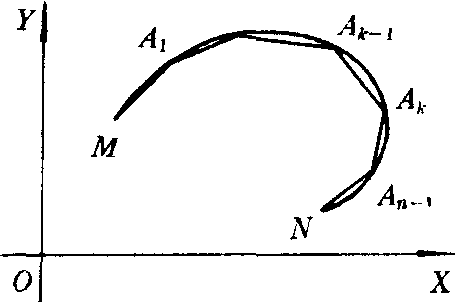
设有平面曲线MN,如图所示. 在曲线MN上任取n—1个点:A1 ,A2,…,Ak-1 ,Ak,…,An-1. 令M=A0,N=Aa .用线段连结相邻的两个点,得到弦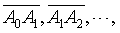
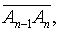 ,这是一条折线. 若当分点无限增加,且每一条弦的长度都趋于零时,折线长度存在极限,则称曲线MN可求长,其长为上述极限值.
,这是一条折线. 若当分点无限增加,且每一条弦的长度都趋于零时,折线长度存在极限,则称曲线MN可求长,其长为上述极限值.
❶若函数f (x)在区间 [a,b]上可导,且导数f' (x)连续,则在 [a,b]上的曲线y=f (x)可求长,且弧长为
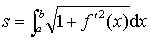
例 求半径为R的圆的周长s,
解 方程x2+ y2 = R2表示一个半径为R的圆. 由对称性知,要求该圆的周长,只需求该圆在第一象限部分的弧长,再四倍即可. 于是
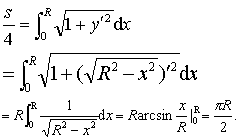
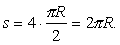
❷若曲线由参数方程 z=φ(t),y= ψ (t),(a≤f≤β)表示,且ψ' ′ (t),ψ' ′ (t)在 [α,β]上连续,则曲线可求长,且弧长为
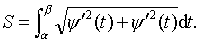
❸若曲线由极坐标方程r=f (θ) (α≤θ≤β)表示,且f' ′ (θ)在 [α,β]上连续,则该曲线可求长,且弧长为
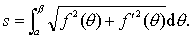
☚ 旋转体的体积 旋转体的侧面积 ☛
- 赵破奴是什么意思
- 赵破奴与匈奴之战是什么意思
- 赵破奴击楼兰、车师之战是什么意思
- 赵硕来是什么意思
- 赵碧琰是什么意思
- 赵磻老是什么意思
- 赵磻老(《全宋词》:ⅲ1629)是什么意思
- 赵礼汉是什么意思
- 赵礼让肥是什么意思
- 赵礼让肥 秦简夫是什么意思
- 赵祖庆是什么意思
- 赵祖康是什么意思
- 赵祖悦是什么意思
- 赵祖铭是什么意思
- 赵祚传是什么意思
- 赵神德是什么意思
- 赵祥星是什么意思
- 赵祥麟是什么意思
- 赵祯是什么意思
- 赵祺是什么意思
- 赵福是什么意思
- 赵福元是什么意思
- 赵福才是什么意思
- 赵福扬是什么意思
- 赵福玉是什么意思
- 赵禹是什么意思
- 赵禹不以贫富取人是什么意思
- 赵禹圭是什么意思
- 赵秀亭是什么意思
- 赵秀君是什么意思
- 赵秀昆是什么意思
- 赵秀治是什么意思
- 赵秀芳是什么意思
- 赵秉均是什么意思
- 赵秉寿是什么意思
- 赵秉德是什么意思
- 赵秉志是什么意思
- 赵秉忠是什么意思
- 赵秉忠状元殿试卷是什么意思
- 赵秉文是什么意思
- 赵秉文《华山》 - 金、元山水诗赏析是什么意思
- 赵秉文《春游》是什么意思
- 赵秉文《虎牢》 - 金、元山水诗赏析是什么意思
- 赵秉文和坡仙赤壁词是什么意思
- 赵秉文的人物故事|评价|小传,赵秉文的事迹|史鉴是什么意思
- 赵秉文行书赵霖昭陵六骏图跋是什么意思
- 赵秉正是什么意思
- 赵秉清是什么意思
- 赵秉理是什么意思
- 赵秉衡是什么意思
- 赵秉钧是什么意思
- 赵秋是什么意思
- 赵秋航是什么意思
- 赵秋舲是什么意思
- 赵秋谷是什么意思
- 赵秋谷所传声调谱是什么意思
- 赵稠等击鲜卑之战是什么意思
- 赵稹是什么意思
- 赵稼书是什么意思
- 赵稼秋是什么意思