平面方程的各种形式pingmian fangcheng de gezhongxingshi
❶普遍式 任何平面可用x,y,z的一次方程ax+by+cz+d=0来表示,反之,x,y,z的一次方程ax+by+cz+d= 0,其中a,b,c是不同时为零的三个任意实数,一定表示一个平面. 这个结论称为平面的基本定理.三元方程ax+by+cz+d=0,a2+b2+c2≠0,称为平面方程的普遍式 (或一般式). 在平面方程的普遍式中,如果常数项不是零,且缺某一个变数,则平面一定平行于该变数所对应的坐标轴; 如果缺某两个变数,则平面一定平行于该两个变数所对应的坐标面. 如果常数项是零,且缺某一个变数,则平面一定过该变数所对应的坐标轴; 如果缺某两个变数,则平面一定是这两个变数所对应的坐标面.
❷ 点法式 已知平面π,过原点和平面π垂直的直线叫做它的法线.法线有两个相反的方向,如果π不过原点,从原点向π作垂线,垂足记为D,射线OD的方向规定为法线的正方向. 如果π过原点,法线的正方向可由第三个方向角γ<90°规定; 如果γ=90°,即π过Z轴,则可由第二个方向角β<90°规定;如果β=γ=90°,即π与YZ面重合,则规定法线的正方向与X轴的正方向一致. 以原点为始点沿平面法线正方向所作的向量叫平面的法线向量. 凡与平面法线平行的非零向量叫平面的法向量.平面法向量的始点是任意的,它的方向与法线的正方向可以相同,也可以相反. 向量形式的平面方程的点法式是: m · (P—P0) =0m≠0,式中m是平面π的一个法向量,P 0是平面π上的一个定点,P是π上的任意一点,P和P0是位置向量,m是自由向量,并且P0和m是常向量,P则是流动向量. 设P 0 (x0,y0,z0),P (x,y,z),m= {a,b,c),a2 +b2+c2≠0,则平面方程坐标形式的点法式为
a (x-x0) +b (y-y0) +c (z-z0) =0a2+b2+c≠0.
❸ 三点式 设已给平面π上三个不共线的点P1(x1,y1,z1),P2 (x2,y2,z2),P3 (x3,y3,z3),则平面π的方程的三点式的坐标形式为
即
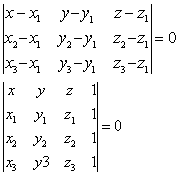
向量形式为
(P—P1 ,P2—P1,P3—P1) =0
式中P= {x,y,z},P1= {x1,y1,z1},P2= {x1,y2,z2),P3= {x3,y3,z3}. 若四个点Pr (xr,yr,zr)(r=1,2,3,4) 中没有三点共线,则它们共面的充要条件是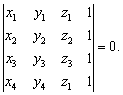
❹ 截距式 过 (a,0,0),(0,b,0),(0,0,c)三点的平面方程的坐标形式是x/a+y/b+z/c=1其中a≠0,b≠0,c≠0.这个方程称为坐标形式的平面方程的截距式,而a,b,c分别叫做平面在三个坐标轴上的截距.
❺ 参数式 已知定点P0 (x0,y0,z0)和过P0的两个不共线的定向量a= {a1 ,a2 ,a3}和b= {b1,b2,b3},则所定平面方程的向量形式是P=P0+ua+vb,-∞
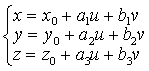 (-∞这两个方程分别叫做向量形式和坐标形式的平面方程的参数式,其中u,v叫做参数.如果已知三个不共线的点P1 (x1,y1,z1),P2 (x2,y2,z2),P3 (x3,y3,z3),则所定平面方程的向量形式是
(-∞这两个方程分别叫做向量形式和坐标形式的平面方程的参数式,其中u,v叫做参数.如果已知三个不共线的点P1 (x1,y1,z1),P2 (x2,y2,z2),P3 (x3,y3,z3),则所定平面方程的向量形式是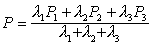 (-∞<λ1,λ2,λ3<+∞,λ1+λ2+λ3=1 )
(-∞<λ1,λ2,λ3<+∞,λ1+λ2+λ3=1 )坐标形式为
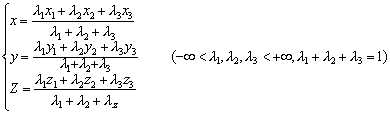
❻ 法线式 已知平面的单位法线向量为N°={cosα,cosβ,cosγ),从原点到平面的距离是p,则向量形式的平面方程的法线式是N°·P-p= 0。坐标形式的平面方程的法线式是xcosα+ycosβ+zcosγ-p= 0,这里cosα,cosβ,cosγ是法线向量的方向余弦。
平面方程的普遍式ax+by+cz+d=0 (a2+b2+c2≠0)的一次项系数a,6,c是这平面法线的一组方向
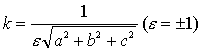 数,叫做法式化因数。(ka,胁b,kc)是法线向量的方向余弦。用法式化因数k去乘平面方程的普遍式,就可以把平面方程化为法线式
数,叫做法式化因数。(ka,胁b,kc)是法线向量的方向余弦。用法式化因数k去乘平面方程的普遍式,就可以把平面方程化为法线式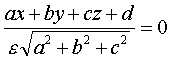
- 宋人酤酒是什么意思
- 宋人金明池争标图页是什么意思
- 宋人集是什么意思
- 宋人雪山行旅图轴是什么意思
- 宋人雪峰寒艇图轴是什么意思
- 宋人雪溪行旅图页是什么意思
- 宋人雪竹图轴是什么意思
- 宋仁是什么意思
- 宋仁圃行述是什么意思
- 宋仁宗是什么意思
- 宋仁宗倡针灸是什么意思
- 宋仁宗曹皇后是什么意思
- 宋仁宗皇后曹氏的人物故事|评价|小传,宋仁宗皇后曹氏的事迹|史鉴是什么意思
- 宋仁楚是什么意思
- 宋仁甫是什么意思
- 宋仁贤是什么意思
- 宋介是什么意思
- 宋代是什么意思
- 宋代“以文为教”政策的失误是什么意思
- 宋代 《诗经》学是什么意思
- 宋代一品卤簿是什么意思
- 宋代七宝辇制是什么意思
- 宋代三司检法等官俸是什么意思
- 宋代三品卤簿是什么意思
- 宋代上尊号仪是什么意思
- 宋代两税是什么意思
- 宋代乡兵制是什么意思
- 宋代乡饮礼是什么意思
- 宋代二品卤簿是什么意思
- 宋代五大名窑是什么意思
- 宋代五车制是什么意思
- 宋代京府属官俸是什么意思
- 宋代亲王群臣车辂制是什么意思
- 宋代亲试进士条制是什么意思
- 宋代以后妇女的礼服是什么意思
- 宋代伞制是什么意思
- 宋代佃主互犯法是什么意思
- 宋代作家是什么意思
- 宋代保任制是什么意思
- 宋代保甲法是什么意思
- 宋代元随傔人衣粮是什么意思
- 宋代先蚕礼是什么意思
- 宋代入内内侍省内臣叙迁制是什么意思
- 宋代入内内侍省诸官俸是什么意思
- 宋代入吊奠仪是什么意思
- 宋代入官制是什么意思
- 宋代入閤仪是什么意思
- 宋代公主下降礼是什么意思
- 宋代公主受封礼是什么意思
- 宋代公主笄礼是什么意思
- 宋代公卿俸禄是什么意思
- 宋代兵制是什么意思
- 宋代内侍省内常侍等官俸是什么意思
- 宋代内外命妇车是什么意思
- 宋代内客省等官俸禄是什么意思
- 宋代册制是什么意思
- 宋代册命亲王大臣礼是什么意思
- 宋代册皇太子仪是什么意思
- 宋代册立皇后仪是什么意思
- 宋代农业是什么意思