导数的几何意义dacshu de jibe yiyi

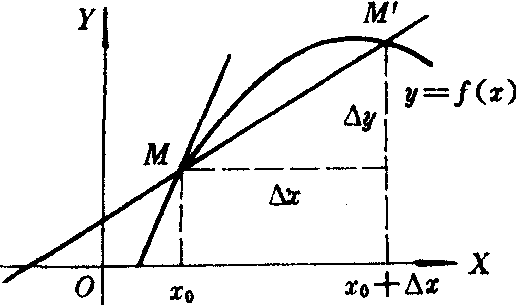
设M (x₀ ,f(x₀) 与M′ (x₀+Δx,f (x₀+Δx)) 是曲线y=f (x)上的两点，则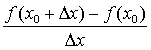表示曲线y=f ( x)的割线MM′ 的斜率。若导数f′ (x₀)存在，则f′ (x₀)表示曲线y=f (x)在点M (x₀,f (x₀))处的切线的斜率 （如上图）。

若f ′ (x₀)存在，则曲线y=f (x)在点M (x₀,f (x₀))处的切线方程是y=f (x₀)=f′ (x₀) (x - x₀)。
若f′ (x₀)存在且不等于零，则曲线y=f (x)在点M (x₀,f(x₀))处的法线方程是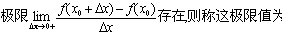(x～x₀)。