对称方程
对称方程duicheng fangcheng
若数域F上含有x1,x2,…,xn的解析式f(x1,x2,…,xn),对于1,2,…,n的任一个排列i1,i2,…,in都有f(x1,x2,…,xn)≡f(xi1,xi2,…,xin),则称f(x1,x2,…,xn)为关于x1,x2,…,xn的对称式.
若一个n元方程f(x1,x2,…,xn)=0中,f(x1,x2,…,xn)是关于x1,x2,…,xn的对称式,则称这个n元方程为对称方程.例如x+y=2,xy=1,x2+y2=3,x2y+xy2=0,(x+y+z) (xy+yz+zx)-3xyz=1等,都是对称方程.
在中学数学里,一般只研究某些特殊的二元对称方程和三元对称方程,以及由它们组成的对称方程组.
若对称式f(x1,x2,…,xn)是一个对称多项式,则f(x1,x2,…,xn)可以由它的初等对称多项式
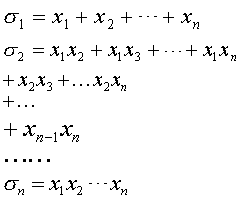
例如,解方程组
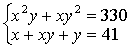
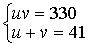
☚ 最简对数方程 倒数方程 ☛
- 善本戏曲丛刊是什么意思
- 善本目录是什么意思
- 善本碑帖录是什么意思
- 善本碑帖录是什么意思
- 善桥是什么意思
- 善模善样是什么意思
- 善气迎人是什么意思
- 善气迎人是什么意思
- 善法是什么意思
- 善法寺舍利塔记是什么意思
- 善游者溺,善骑者堕是什么意思
- 善游者溺,善骑者堕是什么意思
- 善用兵者攻其爱是什么意思
- 善用兵者,修道而保法,故能为胜败之政是什么意思
- 善用兵者,屈人之兵而非战也,拔人之城而非攻也,毁人之国而非久也,必以全争于天下,故兵不顿而利可全,此谋攻之法也是什么意思
- 善用兵者,役不再籍,粮不三载是什么意思
- 善用兵者,无不正,无不奇是什么意思
- 善用兵者,譬如率然;率然者,常山之蛇也。击其首则尾至,击其尾则首至,击其中则首尾俱至是什么意思
- 善男信女是什么意思
- 善男信女是什么意思
- 善男信女是什么意思
- 善的求索是什么意思
- 善的理念是什么意思
- 善的研究是什么意思
- 善的研究是什么意思
- 善的研究(汉译世界学术名著丛书)是什么意思
- 善眉善眼是什么意思
- 善知识是什么意思
- 善知鸟丛书是什么意思
- 善竹桥是什么意思
- 善终是什么意思
- 善终正寝是什么意思
- 善继上人血书华严经是什么意思
- 善缘是什么意思
- 善罢甘休是什么意思
- 善罢甘休是什么意思
- 善罢甘休是什么意思
- 善罢甘休是什么意思
- 善罪身者民不得罪也是什么意思
- 善耆是什么意思
- 善耆是什么意思
- 善耆是什么意思
- 善胜是什么意思
- 善自为谋是什么意思
- 善自为谋是什么意思
- 善自为谋是什么意思
- 善自为谋是什么意思
- 善良是什么意思
- 善良、正直是什么意思
- 善良意志是什么意思
- 善良温顺是什么意思
- 善良管理人注意义务是什么意思
- 善菜是什么意思
- 善行录是什么意思
- 善行无辙迹轴是什么意思
- 善见律是什么意思
- 善见律卷是什么意思
- 善计者是什么意思
- 善诱文是什么意思
- 善说金珠是什么意思