对数求导法
对数求导法duishu qiudaofa
是适用于某些类型函数的求导方法。先将函数y=f (x)两边取绝对值,然后对等式两边取自然对数,变成隐函数形式,最后利用隐函数求导法则求出导数f′ (x),这种方法称为对数求导法。
对数求导法通常用于求以下两类函数的导数。
❶幂指函数y=u (x)v(x )(其中u (x),v (x)都是x的可导函数,且u (x) >0;
❷ 由多次乘除运算和乘方、开方运算得到的函数。
对数求导法的作用在于将积、商与幂指函数的求导运算分别化为和、差与积的求导运算,以便简化运算。
例1 求y=xx (x>0) 的导数。
解 对y=xx两边同时取对数,有
lny = xlnx。
两边同时对x求导,有y′/y=lnx+1
所以 y ′=y (1nx+1) =x x (lnx+1)。例2 求函数
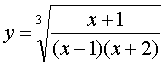 的导数。
的导数。解 取
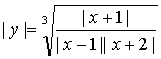
对等式两边取对数,得
ln|y|=1 /3 [ln|x+1}-ln|x-1|-ln|x+2|]
两边对x求导,有
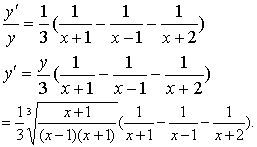
☚ 隐函数的求导法 导数基本公式表 ☛
- 杨石先是什么意思
- 杨石先是什么意思
- 杨石朗是什么意思
- 杨石朗是什么意思
- 杨石魂是什么意思
- 杨石魂是什么意思
- 杨石魂是什么意思
- 杨石魂是什么意思
- 杨石魂是什么意思
- 杨碧秋是什么意思
- 杨碧霞是什么意思
- 杨磊是什么意思
- 杨祐是什么意思
- 杨祖宏是什么意思
- 杨祖武是什么意思
- 杨祖清是什么意思
- 杨祝玲是什么意思
- 杨祥发是什么意思
- 杨祥娣是什么意思
- 杨福同是什么意思
- 杨福基是什么意思
- 杨福家是什么意思
- 杨福家是什么意思
- 杨福庆是什么意思
- 杨福愉是什么意思
- 杨福愉是什么意思
- 杨福昌是什么意思
- 杨福洲是什么意思
- 杨福涛是什么意思
- 杨福涛是什么意思
- 杨福涛是什么意思
- 杨福生是什么意思
- 杨福禄是什么意思
- 杨福绵是什么意思
- 杨福茂是什么意思
- 杨福魁是什么意思
- 杨福魁是什么意思
- 杨福鹏是什么意思
- 杨福鹏是什么意思
- 杨禹廷是什么意思
- 杨禹昌是什么意思
- 杨禹昌是什么意思
- 杨秀山是什么意思
- 杨秀山是什么意思
- 杨秀山是什么意思
- 杨秀峰是什么意思
- 杨秀峰是什么意思
- 杨秀峰是什么意思
- 杨秀峰是什么意思
- 杨秀峰是什么意思
- 杨秀峰是什么意思
- 杨秀峰是什么意思
- 杨秀峰是什么意思
- 杨秀峰教育文集是什么意思
- 杨秀清是什么意思
- 杨秀清是什么意思
- 杨秀清是什么意思
- 杨秀清是什么意思
- 杨秀清是什么意思
- 杨秀清是什么意思