三角形相似的条件

---

1．三个角对应相等，三边对应成比例的两个三角形相似．

2．两角对应相等的两个三角形相似．

3．三边对应成比例的两个三角形相似．

4．两边对应成比例且夹角相等的两个三角形相似．

例1 如图，在△ABC中，D、E、F分别为AB、AC、BC边上的点，且DE∥BC，DF∥AC，找出图中相似的三角形，并说明理由．

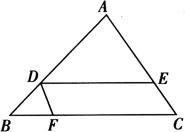
解 理由是

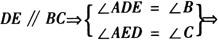
△ADE∽△ABC．

同理可得：

△DBF∽△ABC；

△DBF∽△ADE．

[解析] 根据两角对应相等判定两个三角形相似．

例2 在△ABC与△A′B′C′中，若∠A=60°，AB=4cm，AC=8cm，∠A′=60°，A′B′=11cm，A′C′=22cm，那么△ABC与△A′B′C′是否相似?

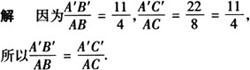
又∠A=∠A′，

所以△ABC∽△A′B′C′．

例3 如图Rt△ABC中，CD是斜边AB上的高，DE、DF分别是△ACD和△BCD的中线，则图中一定相似的三角形共有( )．

A．3对

B．4对

C．5对

D．6对

答 C．

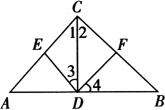
[解析] 由题意可知：

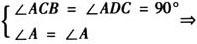
△ADC∽△ACB．

同理△ACB∽△CDB．

根据同角的余角相等可得

∠1=∠B，∠2=∠A．

根据直角三角形斜边上中线等于斜边的一半，可得DE=CE=AE，DF=CF=BF，

∴∠1=∠3，∠B=∠4．

∵∠1=∠B，

∴∠1=∠3=∠B=∠4．

∴△CED∽△BFD，同理△CDF∽△ADE．

即5对相似三角形．