对偶问题dual problem

原始最大化与最小化线性规划问题的相对称问题。对偶性概念之重要在于：
❶解对偶性问题往往比解原来的问题（即原始问题）要容易。
❷得到对偶解就能用它来测定在放宽各种约束条件的场合下会给企业增加多少利润。

对偶问题

实质相同但从不同角度提出不同提法的一对问题。对偶现象是许多管理与工程实际中存在的一种普遍现象。例如，企业怎样充分利用现有人力、物力去完成更多的任务和怎样用最少的人力、物力消耗去完成给定的任务，就是互为对偶的一对问题。对偶理论是从数量关系上研究这些对偶问题的性质、关系及其应用的理论和方法。一个线性规划问题，都存在一个与之相联系的对偶问题。典型的资源利用问题线性规划模型为：

它的对偶模型为：

式中yj代表对偶决策变量，简称对偶变量。线性规划原问题与对偶问题在模型上的一般对应关系如下表：

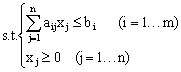
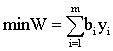
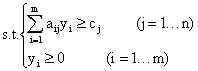
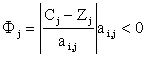
原始问题 （或对偶问题）	对偶问题 （或原始问题）
目标函数max化 约束条件个数m 决策变量个数n 约束条件 决策变量 约束形式“≤”或“≥” 约束形式“=” 变量非负Xj≥0 变量无非负限制，Xj自由变量	目标函数min化 对偶变量个数m 对偶约束个数n 对偶变量 对偶约束条件 对偶变量非负，yj≥0 对偶变量无非负限制，yj自由变量 对偶约束形式“≥”或“≤” 约束形式“=”

有了上述关系，能很方便地写出任何一个线性规划模型的对偶模型来。线性规划模型的对偶性，对线性规划模型理论、求解有着很重要的意义。特别在应用上，线性规划对偶问题的最优解，就是资源的影子价格 (见“影子价格”)，它对于线性规划模型的经济分析，用于对经济管理工作的指导起了极为重要的作用。