完全数wanquanshu

设n是一个正整数，若n的全部正因数的和等于2n，则n就叫做一个完全数.例如6和28都是完全数.因为6的正因数的和为1+2+3+6=6×2;28的正因数的和为1+2+4+7+14+28=28×2.此外，496,8 128也是完全数.
寻求偶完全数的问题与莫森素数密切相关.若M_p＝2^p-1是莫森素数，则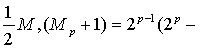-1)是一个偶完全数，而且除此之外没有其他形状的偶完全数.因此寻求偶完全数的问题就归结为寻求莫森素数的问题.因此，是否存在无穷多个偶完全数的问题也是一个未解决的数论难题.
关于完全数的另一个著名难题是，是否存在奇完全数.这个问题至今没有解决，目前已经知道的最好结果是，如果n是一个奇完全数，则n至少有8个不同的奇素因数.此外还证明了，若n是奇完全数，则n>10⁵⁰.由此可见，若奇完全数确实存在，它将是一个很大很大的数.

完全数Wanquanshu

也译作“完美数”(perfectnumber)，指等于自身全部真因数(包括1)之和的数。最小的完全数是6与28:
6=1+2+3,

28=1+2+4+7+14.

有的学者认为， 完全数是古希腊的毕达哥拉斯(Pythagoras，约公元前572—前497年)发现的，但相当多的学者认为， 印度人和希伯来人在更早的时候已经知道6与28是完全数了。
古希腊人非常重视完全数。公元前300年左右，欧几里得在他的名著《几何原本》中证明：只要2ⁿ-1是素数，2^n-1· (2ⁿ-1)就是完全数。显然，这样得到的完全数都是偶数。18世纪， 欧拉 (L. Euler, 1707—1793, 瑞士) 证明： 所有的偶完全数必有上述形式。
容易知道，如果2ⁿ-1是素数，则n必为素数。大约在1634年， 法国人默森尼 (M. Mersenne, 1588—1648) 讨论了形如2n-1(p是素数) 的数， 因此， 后人称这种类型的数为默森尼数， 当它恰好是素数时就称为默森尼素数。于是，由前面所说，偶完全数与默森尼素数 一一对应。
希腊人还研究了与完全数有关的另外两个概念。考虑9和12的全部真因数之和：
1+3=4<9

1+2+3+4+6=16>12

像9这样大于其真因数之和的数叫做亏数 （不足数）；像12这样小于其真因数之和的数叫做盈数（过剩数）。
公元100年左右， 希腊数学家尼科马修斯(Nicomachus) 在他的名著《算术入门》中给出了前4个完全数： 6, 28, 496, 8 128, 并且写道： “也许是这样：正如美的、卓绝的东西是罕有的，是容易计数的，而丑的、坏的东西却滋蔓不已；所以盈数和亏数非常之多，杂乱无章，它们的发现也毫无系统。但是完全数则易于计数， 而且又顺理成章……。它们具有一致的特性： 尾数都是6或8, 而且永远是偶数。”在这段话中包含了三个天才的猜测：
❶完全数非常稀少。确实，到1990年止，人们只发现了30个默森尼素数，于是也就有30个偶完全数。第30个默森尼素数是2²¹⁶⁰⁹¹-1，有65050位，是1985年发现的，由此可知第30个偶完全数有13万多位。随之而来的一个问题是： 偶完全数的个数是有限的还是无穷的？ 这个问题至今尚未得到解决。

❷偶完全数的尾数都是6或8。这一猜测直到18世纪才为大数学家欧拉所证明。

❸不存在奇完全数。这也是至今尚未解决的著名数论难题之一。但已证明，如果奇完全数存在，必将大得惊人。换言之，在此以内足够宽广的自然数范围内是不存在奇完全数的。
完全数有许多有趣的性质， 例如：
❶它们都能写成连续的自然数之和：
6=1+2+3,
28=1+2+3+4+5+6+7,496=1+2+3+4+……+31,

8 128=1+2+3+4+……+127,

❷它们的全部因数的倒数之和都是2:
此外， 完全数还和数论中的许多重要课题有着密切的联系。