回归预测

是由英国生物学家高尔登最初提出的名词。他在研究人类的身高时，发现子女的身高有低于其高个子父母的趋势，而矮个子父母的子女，却往往有高于其父母的趋势。从整个人口来看，高个子的人回归于人口的平均身长；而矮个子的人则作相反的回归于人口的平均身长。高尔登所创用的回归这个名词，以后为许多生物学家和统计学家所沿用。
现在一般把回归两字用来表明一种现象由于另一种现象的变化而发生变化。根据某一个自变量的变动，来推测另一个因变量变动的方向和程度，就是回归预测。它分为一元（单元）回归预测、多元回归预测和自回归预测等。如在经济预测中国民收入与基建投资，人口增长与住宅建设量等都属于回归预测问题。

回归预测

见“回归分析”条。

回归预测

依据数理统计的回归分析理论和方法，找出因变量与自变量之间的依存关系，并建立起一个回归预测方程的方法。这种预测方法主要有：(1)一元回归预测法。即利用统计数据资料，建立起一元回归方程，以一个已知自变量代入方程来估测因变量（预测目标）的预测方法。其基本步骤和方法是：第一步，分析影响预测目标的有关因素，选定自变量，在诸多因素中找出一个决定性因素，作为自变量；第二步，选择合适的回归模型，建立回归方程，自变量确定以后，可以根据自变量与因变量的统计数据资料，以自变量作为横坐标值，因变量作为纵坐标值，组成一系列数对，在坐标图上画出散点图，直观地判别其图像属于哪一种回归模型；第三步，利用回归方程进行预测；第四步，检验预测结果的可靠性，作出评价。一元回归方程可分为一元线性回归方程和一元非线性方程。一元线性回归方程是一个直线回归方程，其方程式为：Y=a+bx，其中Y为预测目标变量，又称因变量；x为影响因素，又称自变量，一般为可控变量；a,b为回归系数。用最小二乘法所得出的公式来求出a, b:a=-; b=n∑xy-∑×∑y/n∑x²-(∑x)²。式中，n为资料个数；∑为求和符号；x,y为变量的历史资料值；、分别为x、y的算术平均数。一元非线性回归方程的一般公式有：指数函数模型：y=ab^x；幂函数模型：y=ax^b；抛物线函数模型：y=a+bx+cx²；双曲线函数模型：y=a+b/x；变形双曲线模型y=x/a+bx。其中a、b、c都是参数。(2)多元回归预测法。即利用统计资料，建立起多元回归方程，以已知两个以上的自变量代入方程来估测另一个因变量（预测目标）的预测方法。多元回归方程，是用来表达一个因变量与多个自变量之间的相关关系及其变动规律性的一种数学模型，其方程式为：y=b₀+b₁x₁+b₂x₂+……b_kx_k，其中，y为预测目标，又称因变量；x₁,x₂……x_k为影响因素，又称自变量；b₀,b₁,b₂……b_k为回归系数。其预测步骤为：建立回归方程；用复相关系数检验方程的显著性；对各自变量进行显著性的检验；进行点估计和区间估计。多元回归方程可分为多元线性回归方程和多元非线性回归方程。

回归预测

分析各种现象之间的数量关系，从与预测对象有密切关系的现象的发展变化，去推测预测对象在未来时间上当相关现象处于某种状态时的数量表现。即建立描述预测对象y和相关因素x数量关系的回归方程式，用一定方法估计方程式中的参数，通过统计检验后，将预测期的相关因素x0代入方程， 可得回归值ŷ₀。ŷ₀便是x₀处观察值y₀的预测值。而实际观察值y₀可能比ŷ₀大， 也可能比ŷ0小，将以1-α的概率落在一定的区间内。可以证明，y0在显著性水平α下的估计区间为：

式中的tα/2值可按自由度n-2由t分布表查得。可见，由回归方程预测y值时，其精度与x0和n有关。当确定回归方程的数据个数 n很大， 且x₀离较近时， 求S值公式可近似为：

这时，y0的估计区间为：
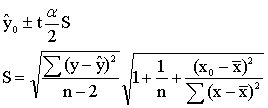
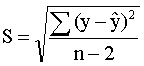
ŷ₀±S 可靠程度为1-α=68.3%
ŷ±2S 可靠程度为1-α=95.4%
ŷ±3S 可靠程度为1-α=99.7%
扩大估计区间，可以提高预测的可靠程度，但如果估计区间很宽，就会使预测结果没有多大意义。