同余tongyu

整数集的一种二元关系.对于给定的正整数m，若用m去除两个整数a和b所得的余数相同，则称a,b对模m同余，记作a≡b (modm)；若余数不同，则称a,b对模m不同余，记作a≢b(modm).在日常生活中，我们所要注意的常常不是某些整数，而是这些整数用某一固定整数去除所得的余数，例如几点钟就是用24去除某个总的时数所得的余数，又例如星期几就是用7去除某一个总的天数所得的余数.由此可见，同余概念是从人们实践活动中抽象出来的数学概念.
容易看出，a≡b (modm)，或m|a-b，或a=b+mk(k为整数)，是a与b有同一关系的三种不同表达方式.
从同余的定义出发，立即可以得到它的下述性质：
❶a≡a(modm) （反身性）;
❷若a≡b (modm)，则b≡a (modm)（对称性）;
❸若a≡b (modm),b≡c(modm)，则a≡c(modm)（传递性）.因此对整数集合来说，同余是一个等价关系.对于给定的任一正整数m，利用“模m同余”这个关系，可以把全体整数进行分类.

同余Tongyu

给定自然数n，如果对于整数a和b有a=n·q₁+r₁ (0≤r₁2+r₂ (0≤r₂1＝r₂，我们就说a与b对于模n同余，记作a≡b(modn)。上式叫做同余式， 读作“a与b对于模n同余”，或读作“对于模n,a与b同余”。例如，35和43被8除，得到的余数都是3，我们就说35与43对于模8同余， 记作35≡43 (mod8)。
a与b对于模n同余的充要条件是：a与b的差能被n整除， 即n|a-b。
同余的概念在日常生活中时常用到，例如“每星期三上体育课”就是用了对于模7的同余的概念。又如，1991年元旦是星期二，问1992年元旦是星期几？因为1991年是平年， 有365天， 而365=7×52+1, 所以1992年元旦应是星期三， 这实际上也是一个对于模7的同余问题。
根据同余的概念和整除性定理， 可以得到以下关于同余的性质：
❶a≡a(modn)（自反性）;
❷如果a≡b (modn)，那么b≡a(modn) （对称性）;
❸如果a≡b (modn), b≡c (modn), 那么a≡c (modn) （传递性）;
❹如果a≡b (modn),c≡d (modn), 那么a+c≡b+d (modn), a-c≡h-d (modn);
❺如果a≡b(modn), c≡d (modn), 那么ac≡bd (modn)。例1:求5013被7除所得的余数。因为50≡1 (mod7)，所以50¹³≡1¹³(mod7), 即50¹³≡1 (mod7), 故50¹³被7除所得的余数是1。例2:如果整数a和b被9除所得的余数分别是r₁和r₂, 则a和b这两个数的积与两个余数的积对于模9同余。因为a≡r1 (mod9), b≡r2(mod9)，所以ab≡r₁r₂(mod9)。例3: 任何正整数与
它的各位数字的和对于模9同余。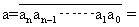
a_n·10ⁿ+a_n-₁·10^n-1+……+a₁·10+a₁，因为10≡1(mod9)，所以10ⁿ≡1 (mod9),a_n·10ⁿ≡a_n(mod9)，……，a₁·10≡a₁(mod9),a₀≡a₀(mod9)，因此 a_n·10ⁿ+a_n-₁10^n-1+……+a₁·10+a₀≡a_n+……+a₁+a₀(mod9), 即a≡a_n+……+a₁+a₀ (mod9)。
由上述例2和例3, 我们可以得出一个常拥的检验正整数计算的方法一弃九验算法（简称弃九法）:设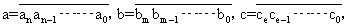如果a_n+a_n-₁+……+a₀(b_n+b_n-₁+……+b₀) ≠(c_e+c_e-₁+……+c₀)(mod9)，那么ab≠c。例：用弃九法检验12345×67891=838114385的正确性。因为12345≡1+2+3+4+5≡6 (mod9), 67891≡6+7+8+9+1≡4(mod9),838114385≡8+3+8+1+1+4+3+8+5≡5mod9, 4×6=24, 245 (mod9), 所以12345×67891≠838114385，原等式不正确。弃九法的优点是验算速度快， 但应特别注意的是当使用弃九法时， 如果 (a_n+a_n-1+……+a0) (b_m+b_m-1+……+b0) ≡ (c_e+c_e-1+……+c0) (mod9), 也不能肯定ab=c是正确的。例如，21×5=114显然是错误的，但3×5≡15≡6(mod9), 114≡6(mod9), 用弃九法检验无效。

同余

congruence