各实验组与对照组均数比较

在一个实验中设k (k>2)个处理组，其中k-1个实验组，一个共同的对照组。实验结果经方差分析各组均数间有差别，进一步作两两比较时，若只需将实验组与对照组比较，而各实验组间不作相互比较时，可用Dunnett检验(C. W. Dunnett,1955)。它与 “多个样本均数间的两两比较”类似，但标准误的计算方法不同。
Dunnett检验的方法步骤如下：
(1) 列出各组均数及方差分析表，将各组 （包括对照组）均数按大小顺序排列，列出对比组及对比范围内的组数a。如将表3的均数排列为：

各对比组为C与甲、C与乙、C与丙，相应的a为2、3、4。
(2) 计算各实验组与对照组均数之差T-C。
(3) 计算T-C的标准误sT-C。若对比的实验组例数nT与对照组例数nC相等时用式(1)，不等时用式(2)。

式中MS组内为方差分析表中的组内均方，式(1)中n为每组例数。
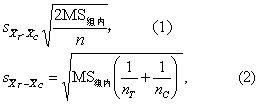
(4) 计算各对比组的统计量q′值，

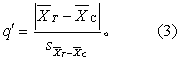
(5) 以组内均方的自由度v和组数a查q′界值表。由于各对比组的a不全相同，故q′界值也不同，是为多重标准。亦有人一律用a=k，得一公用的q′界值，是为单一标准，但界值较大。双侧检验查表1、单侧检验查表2得P值，按所取检验水准作出推断结论。
C. W. Dunnett提出： 当实验组与对照组的方差不齐时，除sT-C的算法与上法不同外， 表1中的界值须作调整；当对照组例数比任何实验组例数均多时，表1中的界值亦须调整，详见表1引文。

表1 Dunnett检验用q′界值表（双侧）
上行：p = 0.05，下行： P=0.01

v	组 数，a
	2	3	4	5	6
5	2.57 4.03	3.03 4.63	3.29 4.98	3.48 5.22	3.62 5.41
6	2.45 3.71	2.86 4.21	3.10 4.51	3.26 4.71	3.39 4.87
7	2.36 3.50	2.75 3.95	2.97 4.21	3.12 4.39	3.24 4.53
8	2.31 3.36	2.67 3.77	2.88 4.00	3.02 4.17	3.13 4.29
9	2.26 3.25	2.61 3.63	2.81 3.85	2.95 4.01	3.05 4.12
10	2.23 3.17	2.57 3.53	2.76 3.74	2.89 3.88	2.99 3.99
11	2.20 3.11	2.53 3.45	2.72 3.65	2.84 3.79	2.94 3.89
12	2.18 3.05	2.50 3.39	2.68 3.58	2.81 3.71	2.90 3.81
13	2.16 3.01	2.48 3.33	2.65 3.52	2.78 3.65	2.87 3.74
14	2.14 2.98	2.46 3.29	2.63 3.47	2.75 3.59	2.84 3.69
15	2.13 2.95	2.44 3.25	2.61 3.43	2.73 3.55	2.82 3.64
16	2.12 2.92	2.42 3.22	2.59 3.39	2.71 3.51	2.80 3.60
17	2.11 2.90	2.41 3.19	2.58 3.36	2.69 3.47	2.78 3.56
18	2.10 2.88	2.40 3.17	2.56 3.33	2.68 3.44	2.76 3.53
19	2.09 2.86	2.39 3.15	2.55 3.31	2.66 3.42	2.75 3.50
20	2.09 2.85	2.38 3.13	2.54 3.29	2.65 3.40	2.73 3.48
24	2.06 2.80	2.35 3.07	2.51 3.22	2.61 3.32	2.70 3.40
30	2.04 2.75	2.32 3.01	2.47 3.15	2.58 3.25	2.66 3.33
40	2.02 2.70	2.29 2.95	2.44 3.09	2.54 3.19	2.62 3.26
60	2.00 2.66	2.27 2.90	2.41 3.03	2.51 3.12	2.58 3.19
120	1.98 2.62	2.24 2.85	2.38 2.97	2.47 3.06	2.55 3.12
∞	1.96 2.58	2.21 2.79	2.35 2.92	2.44 3.00	2.51 3.06

摘自 Dunnett CW: New tables for multiple compa-risons with a control,Biometrics,20: 482,1964

表2 Dunnett检验用q′界值表（单侧）
上行：P=0.05，下行： P= 0.01

v	组 数， a
	2	3	4	5	6
5	2.02 3.37	2.44 3.90	2.68 4.21	2.85 4.43	2.98 4.60
6	1.94 3.14	2.34 3.61	2.56 3.88	2.71 4.07	2.83 4.21
7	1.89 3.00	2.27 3.42	2.48 3.66	2.62 3.83	2.73 3.96
8	1.86 2.90	2.22 3.29	2.42 3.51	2.55 3.67	2.66 3.79
9	1.83 2.82	2.18 3.19	2.37 3.40	2.50 3.55	2.60 3.66
10	1.81 2.76	2.15 3.11	2.34 3.31	2.47 3.45	2.56 3.56
11	1.80 2.72	2.13 3.06	2.31 3.25	2.44 3.38	2.53 3.48
12	1.78 2.68	2.11 3.01	2.29 3.19	2.41 3.32	2.50 3.42
13	1.77 2.65	2.09 2.97	2.27 3.15	2.39 3.27	2.48 3.37
14	1.76 2.62	2.08 2.94	2.25 3.11	2.37 3.23	2.46 3.32
15	1.75 2.60	2.07 2.91	2.24 3.08	2.36 3.20	2.44 3.29
16	1.75 2.58	2.06 2.88	2.23 3.05	2.34 3.17	2.43 3.26
17	1.74 2.57	2.05 2.86	2.22 3.03	2.33 3.14	2.42 3.23
18	1.73 2.55	2.04 2.84	2.21 3.01	2.32 3.12	2.41 3.21
19	1.73 2.54	2.03 2.83	2.20 2.99	2.31 3.10	2.40 3.18
20	1.72 2.53	2.03 2.81	2.19 2.97	2.30 3.08	2.39 3.17
24	1.71 2.49	2.01 2.77	2.17 2.92	2.28 3.03	2.36 3.11
30	1.70 2.46	1.99 2.72	2.15 2.87	2.25 2.97	2.33 3.05
40	1.68 2.42	1.97 2.68	2.13 2.82	2.23 2.92	2.31 2.99
60	1.67 2.39	1.95 2.64	2.10 2.78	2.21 2.87	2.28 2.94
120	1.66 2.36	1.93 2.60	2.08 2.73	2.18 2.82	2.26 2.89
∞	1.64 2.33	1.92 2.56	2.06 2.68	2.16 2.77	2.23 2.84

摘自 Dunnett CW:A multiple comparison prece-dure for comparing several treatments witha control,J. Amer. Statist. Assoc.,50: 1096,1955
例 试验三菱莪术的抑癌作用，将小白鼠分四组，先致癌，然后对甲、乙、丙组依次注药0.5ml、1.0ml、1.5ml，对照组不用药。表3是各鼠的肿瘤重量。问各用药组的瘤重是否减轻？

表3 三个实验组与一个对照组小白鼠的肿瘤重量(g)

对照组		实 验 组
		甲	乙	丙
X	3.6 5.6 4.5 7.0 4.2 4.1 4.4 5.0 3.7 4.5	3.0 3.7 2.3 2.7 2.4 1.9 1.1 2.6 4.0 1.3	0.4 1.3 1.7 3.2 2.3 3.0 4.5 2.1 3.6 2.5	3.3 3.2 1.2 0.6 0.0 1.4 2.7 1.2 3.0 2.1
n	10	10	10	10
	4.66	2.50	2.46	1.87

先就表3资料作方差分析。
H0: μ0=μr₁＝μr2=μr₃
H1:四个总体均数不等或不全相等。
α=0.05。
结果见表4，按α=0.05水准拒绝H₀，接受H₁，可认为四个总体均数不等。将三个实验组均数分别与对照组均数作比较。

表4 表3资料的方差分析

变异来源	SS	v	MS	F	P
总	86.74	39
组 间 组 内	45.09 41.65	3 36	15.0300 1.1569	12.99	<0.01

H₀: μr=μC,
H₁:μT<μC。
单侧α=0.05。
四组均数的大小顺序见表3末行，由此确定各对比的实验组，两均数之差|r-c|及组数α，见表5第(1)、(2)、(3)栏。按式(1)得

按式(3)得各对比组q′值见表5第(4)栏。按v=36及第 (3)栏α，查表2得各P值，见第(5)栏。按α=0.05水准，三种比较均拒绝H0，接受H1，故可认为三个实验组的肿瘤平均重量都低于对照组，即三种剂量的三菱莪术对于小白鼠均有抑癌作用。

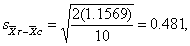
表5 三个实验组与对照组均数的比较

对比的实验组 (1)	|-| (2)	a (3)	q' (4)=(2)/0.481	P (5)
甲 组 乙 组 丙 组	2.16 2.20 2.79	2 3 4	4.49 4.57 5.80	<0.01 <0.01 <0.01

如按单一标准(ν=36,α=4)，上述三种比较仍得P<0.01，结果相同。