古诺均衡
又称“古诺-纳什均衡”。双寡头非合作博弈中,一组最优产量策略的组合。即在给定竞争者的产量的情况下,每个企业都选择其能实现利润最大化的产量。这时,每个企业都没有再单方面改变其产量的冲动。参见“古诺模型”。
古诺均衡
古诺均衡Cournot equilibrium
指这样一组厂商的产出水平和最终市场价格,在这一产出水平和价格下,没有厂商能够在其他厂商生产的古诺产量给定的前提下,通过改变自身的产出水平来提高利润。
先考察两个厂商时的古诺均衡。假定每个厂商的成本函数为TCi(qi)=ciqi,i=1,2,其中c1,c2>0。市场需求函数为P(Q)=a-bQ,a,b>0,a>ci,其中Q=qi+q2。则古诺均衡要求满足两个一阶条件:
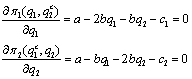
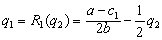
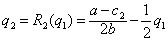
联立方程就可求出古诺均衡解为:
q1c=(a-2c1+c2)/3b
q2c=(a-2c2+c1)/3b
Pc=a-bQc=(a+c1+c2)/3
同时有二阶条件∂2πi/2qi2≤0。 由反应函数可画出反应曲线,两厂商反应曲线的交点为均衡点,两厂商的产量是战略替代的。
模型推广到N个厂商时分两种情况考虑,其一,N个厂商成本相同;其二,N个厂商成本不同。在第一种情况下,有ci=c,i=1,…,N。则对任一厂商i,求
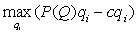
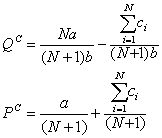
☚ 古诺双寡头 古诺模型 ☛
- 丹霞烂漫是什么意思
- 丹霞烧佛是什么意思
- 丹霞破佛是什么意思
- 丹霞蔽日 彩虹垂天是什么意思
- 丹霞衣是什么意思
- 丹霞观是什么意思
- 丹靈是什么意思
- 丹青是什么意思
- 丹青
 是什么意思
是什么意思 - 丹青不渝是什么意思
- 丹青不知老将至,富贵于我如浮云是什么意思
- 丹青不知老将至,富贵于我如浮云。是什么意思
- 丹青之信是什么意思
- 丹青传象是什么意思
- 丹青初炳而后渝,文章岁久而弥光。是什么意思
- 丹青副是什么意思
- 丹青化去是什么意思
- 丹青变丑妍是什么意思
- 丹青图画飞去无踪是什么意思
- 丹青地是什么意思
- 丹青墨韵—四川省文化馆馆藏书画名家精品集是什么意思
- 丹青妙手是什么意思
- 丹青妙笔是什么意思
- 丹青客是什么意思
- 丹青师傅是什么意思
- 丹青引是什么意思
- 丹青引赠曹将军霸是什么意思
- 丹青引赠曹将军霸 - 唐·杜甫是什么意思
- 丹青引赠曹将军霸 - 杜甫 - 将军魏武之子孙,于今为庶为清门。英雄割据虽已矣,文彩风流今尚存。学书初学卫夫人,但恨无过王右军。丹青不知老将至,富贵于我是什么意思
- 丹青引赠曹将军霸 - 杜甫 - 将军魏武之子孙,于今为庶为清门。英雄割据虽已矣,文采风流今尚存。学书初学卫夫人,但恨无过王右军。丹青不知老将至,富贵于我是什么意思
- 丹青引赠曹将军霸(杜甫)是什么意思
- 丹青彪炳是什么意思
- 丹青怎生画取。是什么意思
- 丹青总录是什么意思
- 丹青手是什么意思
- 丹青无不可,霖雨亦相期。是什么意思
- 丹青泪是什么意思
- 丹青竹是什么意思
- 丹青绝技是什么意思
- 丹青绝技,良深感佩是什么意思
- 丹青记是什么意思
- 丹青谁画真真面。是什么意思
- 丹青辋川是什么意思
- 丹青过实是什么意思
- 丹青难写是精神是什么意思
- 丹青风雅颂—中国历代名画鉴赏是什么意思
- 丹青饮是什么意思
- 丹青魂是什么意思
- 丹頂是什么意思
- 丹頭是什么意思
- 丹頰是什么意思
- 丹顶是什么意思
- 丹顶鹤是什么意思
- 丹顶鹤的传说是什么意思
- 丹顶鹤的第二故乡是什么意思
- 丹颈是什么意思
- 丹颊是什么意思
- 丹颖是什么意思
- 丹飈是什么意思
- 丹飙是什么意思