变异量数measures of variation

表明某项数据资料变异程度或离中趋势的数值。离中趋势如何也是数据分布的一项重要特征。要对数据资料的分布特征进行比较全面的描述，除计算反映集中趋势的平均数以外，还必须计算反映离中趋势的变异量数。变异量数越大，表示数据的离散程度越大，其平均数的代表性就越小。常用的变异量数有：
❶全距(range)，是数据资料中最大数值与最小数值之差，又称极差；
❷四分位差(quartile deviation)，是第三个四分位数（位于中位数和最大数值中间的数值）与第一个四分位数（位于中位数和最小数值中间的数值）之差的1/2的距离；
❸平均差(average deviation)，数据资料的每个数值与其算术平均数之差的绝对值的算术平均数；
❹标准差(standard deviation)，数据资料的每个数值与其算术平均数之差的平方的算术平均数的平方根。这是最重要也最常用的变异量数。标准差的平方，就是方差(variance)。
根据未分组资料计算标准差(σ)的公式为：

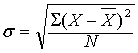
根据频数分布资料计算标准差的公式为：

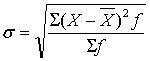
上述各种变异量数的单位，均与原数据资料的单位相同，都属绝对变异量数。为了比较单位不同或虽单位相同但平均数不同的两项数据资料的变异程度或离中趋势，还需计算相对变异量数。最重要也最常用的相对变异量数为标准差系数(coefficient of standard deviation)，它是同一数据资料的标准差与其算术平均数之比率。