双曲线的标准方程shuangquxian de biaozhunfangcheng

指方程.双曲线的标准方程表示焦点为F₁(-c,0)和F₂(c,0)，满足||MF₁|-|MF₂||=2a的点M(x,y)的轨迹(其中b²＝c²-a²)(如图1).这一标准方程的导出过程，表明“双曲线上任意一点的坐标都适合这一方程”；而“坐标适合这一方程的点必在双曲线上”

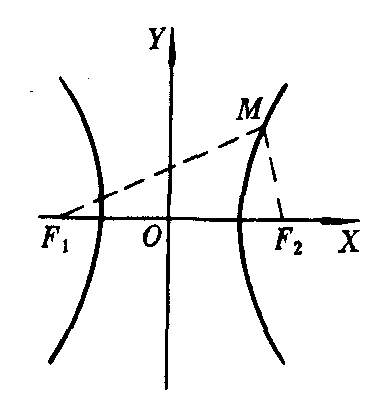
图1

图2

方程

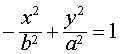
也叫做双曲线的标准方程，表

示焦点为F₁(0,-c)和F₂(0,c)，满足||MF₁|-|MF₂||=2a的点M的轨迹(其中b²＝c²-a²) (如图2).
双曲线的标准方程的特征是：
❶左端只含x²项和y²项，并且系数写在分母的位置上，一项取正号，一项取负号，右端只有常数1;
❷双曲线的中心在原点，焦点在坐标轴上，对称轴是两坐标轴.
中心位于(x₀,y₀)，对称轴平行于坐标轴的双曲线

方程是

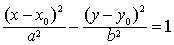
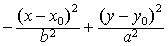＝1.它们的焦点分别是(x₀±c,y₀)和(x₀,y0±c).