参数的点估计
参数的点估计
参数的点估计就是选定一个适当的样本统计量作为参数的估计量,并计算出估计值。如选样本均数作为总体均数的估计量;再由样本数据计算出样本均数的值,作为总体均数的估计值。点估计的常用方法有矩法和极大似然法。矩法,即用样本r阶矩作为总体r阶矩的估计量(参见条目“随机变量”)。极大似然法,即由似然函数确定参数的极大似然估计量(参见条目“极大似然法”)。所用统计量是否适于作参数的估计量,主要有三条衡量的标准:无偏性,一致性和有效性。
无偏性 估计量的值虽不全等于参数,但应要求它在参数值附近摆动。如果一个估计量θ的期望值等于被估计的参数θ值时,即
E( )=θ, (1)
)=θ, (1)
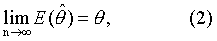
 为θ的渐近无偏估计量。比如当总体为正态分布时,样本统计量
为θ的渐近无偏估计量。比如当总体为正态分布时,样本统计量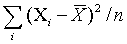 就是总体方差的渐近无偏估计量,但它不是无偏估计量。而样本方差
就是总体方差的渐近无偏估计量,但它不是无偏估计量。而样本方差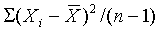 才是总体方差的无偏估计量。
才是总体方差的无偏估计量。一致性 若n愈大,估计量
 的值更集中地分布在参数θ附近,用平方误差来表示为
的值更集中地分布在参数θ附近,用平方误差来表示为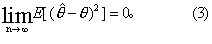
 称作参数θ的一致估计量。由于
称作参数θ的一致估计量。由于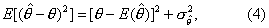
 )]2与
)]2与 的方差σ
的方差σ 2都逼近于零,故[θ-E(
2都逼近于零,故[θ-E( )]逼近于零,由式(1)及式(2)说明
)]逼近于零,由式(1)及式(2)说明 是一个无偏估计量或渐近无偏估计量。 因此若
是一个无偏估计量或渐近无偏估计量。 因此若 是一个无偏估计量, 而且
是一个无偏估计量, 而且 的方差随着样本含量的增大而逼近于零时,则
的方差随着样本含量的增大而逼近于零时,则 是θ的一致估计量。如样本均数X和样本方差s2分别是总体均数μ和总体方差σ2的无偏估计量,而且式(4)右端的两项随着n的增大都逼近于零,所以它们也是一致估计量。
是θ的一致估计量。如样本均数X和样本方差s2分别是总体均数μ和总体方差σ2的无偏估计量,而且式(4)右端的两项随着n的增大都逼近于零,所以它们也是一致估计量。有效性 若
 和
和 ′是参数θ的两个估计量,其中
′是参数θ的两个估计量,其中 与θ的平方误差较小,即
与θ的平方误差较小,即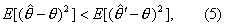
 比
比 '有效。 由式(4)可见,对于两个无偏估计量来说,方差较小的估计量较有效。进一步说,当样本含量确定后,在所有无偏估计量中可能存在一个方差最小的估计量,称为有效估计量。
'有效。 由式(4)可见,对于两个无偏估计量来说,方差较小的估计量较有效。进一步说,当样本含量确定后,在所有无偏估计量中可能存在一个方差最小的估计量,称为有效估计量。估计量的有效性是在样本含量相同的情况下比较不同估计量的精度(分布宽度),如果
 比
比 '更有效,那是指对任何有限含量n,
'更有效,那是指对任何有限含量n, 值的分布比
值的分布比 '值的分布更靠拢参数;而一致性则是指在样本含量n→∞时,估计量的集中趋势。 如果
'值的分布更靠拢参数;而一致性则是指在样本含量n→∞时,估计量的集中趋势。 如果 是θ的一致估计量, 则随着n→∞,
是θ的一致估计量, 则随着n→∞, 值的分布无限的向参数θ集中。
值的分布无限的向参数θ集中。估计量的选择 选择统计量作为某参数的估计量时,通常应尽量选择无偏、有效且一致的估计量。例如,样本均数X是总体均数μ的无偏的、一致的和有效的估计量,因而较常用;若某参数有两个无偏、一致的估计量,一个比另一个更有效,应选更有效者。例如,在对称分布中,样本中位数M也是总体均数μ的无偏的、一致的估计量,但不如样本均数X有效,因此不宜以M代替X。有时,一个估计量虽然更有效,但它的抽样分布太复杂,难于从理论上进行处理,亦可选择一个有效性稍差但易处理的估计量。
☚ 参数估计 极大似然法 ☛
- 职工福利基金是什么意思
- 职工福利基金审计是什么意思
- 职工科普与技术交流是什么意思
- 职工美德是什么意思
- 职工考核是什么意思
- 职工考核方式是什么意思
- 职工考试心理是什么意思
- 职工股是什么意思
- 职工自学心理是什么意思
- 职工自我教育是什么意思
- 职工自我评价是什么意思
- 职工董事和职工监事的权利、义务及其职责是什么意思
- 职工董事和职工监事的管理和保护是什么意思
- 职工董事和职工监事的设置是什么意思
- 职工行为是什么意思
- 职工调配是什么意思
- 职工选聘是什么意思
- 职工道德教育是什么意思
- 职工集体福利是什么意思
- 职工零星调动是什么意思
- 职工食堂管理工作是什么意思
- 职工高等学校招生体格检查表是什么意思
- 职工高等学校招生政治审查表是什么意思
- 职役是什么意思
- 职役是什么意思
- 职役是什么意思
- 职役是什么意思
- 职役是什么意思
- 职役是什么意思
- 职志是什么意思
- 职思其忧是什么意思
- 职思堂法帖是什么意思
- 职掌是什么意思
- 职方是什么意思
- 职方是什么意思
- 职方外纪是什么意思
- 职方外纪是什么意思
- 职方氏是什么意思
- 职方氏是什么意思
- 职方氏是什么意思
- 职方考镜是什么意思
- 职方郎中是什么意思
- 职权是什么意思
- 职权是什么意思
- 职权是什么意思
- 职权是什么意思
- 职权是什么意思
- 职权是什么意思
- 职权主义是什么意思
- 职权主义是什么意思
- 职权主义诉讼是什么意思
- 职权原则是什么意思
- 职权原则是什么意思
- 职权原则是什么意思
- 职权影响力是什么意思
- 职权根据追查令是什么意思
- 职权立法是什么意思
- 职权立法是什么意思
- 职次是什么意思
- 职此之由是什么意思