印度古代数学Yindu gudai shuxue

古代印度包括今天南亚次大陆的各个国家(巴基斯坦、孟加拉、尼泊尔等)。属于新石器时期的梅赫加尔遗址的发现，使印度文明可以上溯到约公元前6000年，在这一遗址公元前3500年的文化层中出土了绘有多种几何图案的陶瓶。在公元前2200—前1750年的哈拉巴铭文中出现了下面的数字符号：
成书于公元前13—前7世纪的《吠陀》、公元前8—前5世纪的《祭坛建筑》中均含有数学知识。公元5世纪印度数学进入了它发展的高潮时期， 著名的天文数学著作《苏利耶历数全书》成书于5世纪初， 由70页贝叶组成的《巴克沙利手稿》是一部数学专著，大约完成于四、五世纪， 但也许迟至八、九世纪。
印度数学的主要成就在算术与代数方面， 最突出的贡献是发明了十进位值制的数码与表示空位的零号(参见“印度—阿拉伯数码”)最著名的数学家有阿耶波多 (Aryabhaia I, 约 476—550)、婆罗摩笈多(Brahmagupta，约598—约665)，摩诃毗罗(Mahavira,9世纪)、婆什迦罗 (Bhaskara Ⅱ, 1114—约1185)。
印度人很早就建立了整数与分数的四则运算， 在《吠陀》中已出现二次不尽根的近似计算，《祭坛建筑》
(=1.414215686)。628年， 婆罗摩笈多在其名著《婆罗摩修正体系》中讨论了零的运算、正负数的运算以及无理数的运算法则，并运用了四项比例算法。他是世界上最早研究零的运算性质的数学家。但是，关于零除数的认识遇到了 一些困难、9世纪的摩诃毗罗仍然认为一个数除以零数值不变， 直到婆什迦罗才正确地指出一个（非零） 数除以零将导致无穷大量。
从《巴克沙利手稿》与婆罗摩笈多的著作中可以看出， 印度人很早就开始用缩写文字和一些记号来表述与处理代数问题， 婆什迦罗的著作则是印度缩写代数的代表作。由于符号的使用，使印度的代数学获得了极大的便利。印度人广泛使用了试位法，掌握了一些特殊类型的线性方程组解法。阿耶波多给出不少重要的级数求和公式。如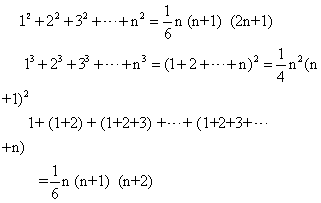

婆罗摩笈多深入研究了等差数列， 并给出了 二次方程求一个正根的公式。婆什迦罗已经认识到二次方程有两个根，但总是舍去负根，他还用配方法解出了某些特殊的三次方程。大约在11世纪，印度人得到了“金字塔图”，即二项式系数表，在此之前他们已经有了初步的排列组合知识， 并可能由此导出金字塔图。
印度人在求解不定方程方面颇有成就。他们把求一次不定方程
ax+c=by (a, b) =1
的正整数解的方法称为“库塔卡”，意为“碾细”。他们还研究了一次不定方程组， 以及形如
Nx²+1=y² （贝尔方程）
与 cy²＝ax²+b
的二次不定方程， 还给出了整勾股数的一个特殊公式x:y:z= (a²-1) :2a: (a²+1)。
印度早期的《祭坛建筑》中含有一些简单的面积、体积计算问题，并且使用了勾股定理。阿耶波多给出了一个相当精确的圆周率值3.1416，后来被婆什迦罗称为密率， 并称22/7为实用率或粗率。婆罗摩笈多 （参见该条）给出了圆内接四边形的两个重要公式，婆什迦罗证明了勾股定理并给出了正确的球体积与表面积公式。
印度人继承了希腊人的三角学知识， 并将希腊的全弦改为半弦（相当于正弦线）,8世纪初曾传入中国。
有许多迹象表明， 印度数学受到了中国数学的影响，既有一般的数学原理、方法与结果，也有许多具体的数学问题，还曾将这种影响传播到阿拉伯与欧洲。至于印度数学本身对阿拉伯、欧洲及唐代以前中国数学的影响， 则是众所周知的。