卫生事业管理中的数学方法

应用数学方法提高卫生事业管理水平以达到高质量、高效能、低费用的要求，是现代科学技术发展的必然趋势。数学方法在卫生事业的计划管理、业务控制、综合评价、费用效果分析、预报预测等方面有较大的应用价值。
辩证唯物主义体现的物质世界普遍联系及其整体性的思想，就是系统思想。现代科学技术对于系统思想方法是有重大贡献的。第一个贡献在于使系统思想方法定量化，成为一套具有数学理论、能够定量处理系统内各组成部分联系的科学方法； 第二个贡献在于为定量化系统思想方法的实际应用提供了强有力的计算工具——电子计算机。这两大贡献都是在二十世纪中期实现的。华罗庚教授从六十年代初期在全国大力推广“统筹法”。1978年中国科技工作者提出了利用系统思想把运筹学和管理科学统一起来的见解。国外在这些方面也有较大的发展。满意地解决复杂系统的规划、设计、管理及控制问题，需要采用系统科学的方法。
系统科学的主要原理 有以下几点。
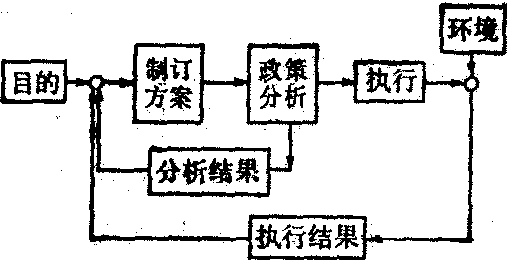
(1)反馈控制原理： 决策者制定政策的过程或执行过程都是反馈控制的过程，即把政策执行的结果 （反馈信息） 与原定目的比较分析，然后再修改政策。有时是多路的反馈控制，比如：

(2) 最优化原理： 在有利的条件下，能取得最大的效果（包括经济效益），而在不利的时候，避免可以避免的损失。
(3) 协调原理与动态系统的稳定性等也是系统科学的原理。
近代系统科学的主要内容有规划论(包括物资储存、人员交替)，排队论，对策论，搜索论等，此外控制论、信息论、质量控制、系统的可靠性与数学模型等也是系统科学涉及到的内容。这些内容相互联系，很难截然区分开来。
各系统一般说来是多因素、多变量、多目标的。复杂的大系统是由许多子系统组成的。在卫生系统中有大量的这种情况存在。作为一个卫生事业的组织者、决策者、管理者，应当具备一定的数学知识，掌握系统科学的基本概念，结合自己的医学知识与实际卫生工作经验，通过各种形式的协作配合，正确应用，以期能从错综复杂的事物平衡中作出决策，把自己的工作建立在科学基础上。
(1) 规划论： 是系统科学中历史较长、较为成熟、应用也最广的一个重要内容。一般可分为静态规划与动态规划两种。静态规划又可细分为线性规划与非线性规划。静态规划是在一个单位时间内，如一个年度的规划，而动态规划是在相连几个单位时期内的规划，因而后者比前者复杂和难解得多。通常所说的规划论是指静态线性规划而言的。处理静态线性规划时常使用图表作业法、解乘数法和单纯形法。
规划论所研究的问题主要有两类： 一类是已经确定了一项任务，采取怎样的方法，才能以最小量的人力和物力来完成；另一类是已经具备了一定数量的人力和物力，怎样去安排和运用，才能完成最大限度的工作量，发挥最大的效果。这两类问题实际上是一个问题的两个不同的提法。解决这两类问题的办法是从数学上进行数量关系的分析，而且总是涉及所谓极值的问题。
例一： 基层卫生机构的设置应根据方便病人服务生产的原则。设某一地区有五个居民点、其居民人数分别为500、1130、2110、2150及5750，经协议拟共同建立一个卫生院。今假定所选地址及房舍不受限制，问这一卫生院设在那儿最合适？
方法： 在一块窗纱上照地形划定五个孔，分别代表这五个居民点，用五条等长的线分别穿过各个孔，在第一孔下面系以一个砝码F1（代表某一居民点人数），穿过其他各孔的线各系以砝码F2、F3、F₄及F₅。然后把五根线在窗纱上面结在一个环上，放手，环落处便是卫生院所在地（注意摩擦力的减少）。最后把它的“相对位置”及“坐标”记录下来即可。
例二：某地区有麻疹患儿访视和体检两项任务，由于争取访视的及时性，必须在一天内完成，剩下来的人员再安排体检。体检任务在一天内不一定全部完成，但完成越多越好。假定全区担任地段保健工作的卫生人员共有45人，其工作效率（每天每人完成人次数）见表中括号内数字。试求一最优人员安排方案。

	访 视	体 检	人 数
医 生 护 士 保健员 任 务	(20) (18) (15) 290人	(40) (30) (20) 1000人	10人 15人 20人 45人

运筹学提供了一个简便的计算方法，帮助我们迅速找出最优的人力安排方案。先按表中数据计算出各种医务卫生人员访视与体检的效率比，结果为：
医生 20:40=0.5
护士 18:30=0.6
保健员 15:20=0.75
安排任务时，就从最大的效率比开始，即先派保健员访视，然后分派护士和医生体检，这种安排方案就完成任务来讲是最优的。
(2) 排队论： 排队论的研究对象是社会中的拥挤现象。排队论主要研究的问题，属于服务质量方面的有等待排队的时间、排队的长度以及等待时间和被接待时间的比例等，此外还有排队系统的费用效能问题。医疗卫生部门是一个服务系统，也即构成了一个排队系统。例如门诊部要经过挂号、诊疗、检验、交费、取药等环节； 医院方面所关心的是如何根据排队的病人数，合理安排调整各项有关设施；病人所关心是如何尽快得到优良服务。排队论的中心目标是寻求组织排队系统的总体最佳方案。既要从医院的医疗工作来设想，又要从病人、接受医疗卫生服务方面来设想，把排队系统组织得合理，以便既保证医疗服务质量，又要做到厉行节约。
排队系统的特征有：
❶输入，如病人到达情况，或称为排队系统的输入。输入就每次到达的病人数来说，有每次1个的，也有每次多个的； 就病人到达的时间间隔来说，有预知的，有随机的，有等间隔的，也有不等间隔的； 就病人来源说，有无限的，也有有限的。
❷输出，就是服务时间的分布状况，或称排队系统的输出。也可以分为常量的、随机的（无法事先肯定的）、预知的等。
❸服务规划。分两种，一是无限制的排队等待，按先后顺序接受服务，其中又存在不同情况，如转诊病人可以有优先权，又如非公费或劳保医疗的城市散居居民可以自由离去。二是排队的长度有一定限制，如定额挂号。
❹服务站数可以是单站的，也可以是多站的。在多站的情况下，又可分为并联、串联和并、串混联等。例如只有一个诊察台（室）的门诊所就是单站系统； 有几个诊察台（室）的可视为多站并联系统； 如在诊察台（室）排队后又要到检验科排队，则两处排队就构成并、串混联系统。排队系统的特征（即排队的决定因素）不同，其与服务质量之间的数量关系必须通过不同的数学模型来表达。例如在最简单排队系统的输入应具有平稳性、无后效性、普通性，常用泊松分布、负二项分布等来分析。
Erlang的微分差分方程法与Lindley积分方程法在处理排队模型时是常用的理论方法。通过抽样方法，利用适当数学模型，可以确定输入与输出分布。这些分布有助于医院对病人做出有用的决策。
(3) 对策论： 对策论是研究形形色色的带有斗争性质的现象。它指示这些现象中的决策人如何采取最优的行动。正确运用对策论，可以确定最有利的策略，作出最好的方案。中国历史上有这样一个著名的例子。战国时，齐王和田忌赛马。他们各有三匹马： 上马、中马、下马。比赛分三场进行，每场以千金为赌注。如果把同级的马来比赛，齐王的马总是能胜过田忌的马，田忌总是失败而且输钱。当时田忌的门客孙膑献计，建议以下马对齐王的上马，以上马对齐王的中马，中马对齐王的下马。比赛的结果是二胜一败，田忌净赢千金。
对策论有静态对策与动态对策两大类。静态对策中又有不结盟对策和结盟对策两种。每种对策又可细分为几种模型。
对策论的应用是很广泛的。在人们向大自然索取资源的斗争中，在除害灭病中都有着应用对策论的可能性。例如某一生产中药材为主的大队共有药地1,300亩，需种13种药材。如何安排一个各种药材的种植计划，使得在水和肥 （劳力与种子等因素可不考虑） 的各种不同的条件下，能够在保证药材生产总量（以满足国家统购的需要）的基础上增加总产值。这个对策问题中对策者为人和大自然。又例如一个医生诊疗某种疾病时，在进行了必要的检查之后，投以某种药物，在获得了病人的反应后，继续投药并观察病情的变化，一直到得出某种结果为止。从开始到结局，医生所采取的一系列治疗措施，也是一个策略。
(4) 数学模型： 不少卫生服务对象可以根据实际资料建立数学模型，再据以指导卫生服务工作。如有某一市区对连续6年人口的出生季节变动作了全面调查。设X代表出生月份，Y代表出生比。出生月份由1月至12月，出生比系每月平均日出生数与全年平均日出生数之百分比。今对六年期间全部调查结果进行综合分析，以多项式方法配以3次曲线，得：

根据这一结果，试回答： 这一期间最高和最低的出生数都在几月份？按微分法求极值，得4月为出生淡季，10月份为出生旺季。
此外，如以出生数概略代表住院接产工作量 (假定住院分娩率为100%)，接产旺季10月份较全年总平均高出百分之几？接产淡季4月份又较全年总平均低了百分之几？经计算得知旺季增加13%，淡季减少14%。作为一个地区卫生行政部门与医院管理人员，在进行业务管理时应充分注意到这一事实所带来的影响。
综合评价方法 系统的好坏必须有一个评价标准，或者说，必须有一个尺度或指标去衡量。如在评价医院工作时，有平均病床周转率高，平均住院日数少，平均每日医疗费用低，平均职工出勤率高，治愈好转率高，住院病死率低，诊断符合率高等等。对于复杂的系统，同时有许多指标，这时不能只用单项指标去评价一个系统，可以用一种综合的评价方法。
质量控制方法 质量控制是检查和保证工作质量的一个重要措施，目前已广泛应用于临床检验、生物检定、动物实验、环境监测、食品卫生监督、医院工作和传染病管理等许多方面。
控制图由中心线与上下范围线组成，按样本顺序或时间顺序逐个将被检指标点在图上。如果点子在范围线以内为“正常”，或说明质量在控制中； 如果点子超出范围线，说明“异常”或表明质量失去控制。这样可以避免单纯满足总结的需要而进行终末分析，从而达到发挥事前控制的作用。
现以某医院外科为例，说明环节质控记分法如下：
(1)将本系统分列为几个环节： 例如可有三级查房、病例讨论、术前讨论、术中质量、术后处理等。
(2) 根据实际情况确定各个环节所需控制的项目。以病史体检为例，可设： 病史询问详细、项目完整、书写端正； 体检全面细致、能抓住重点； 诊断有根据； 治疗有计划； 用药及各种检查得当； 病程记录及时、真实；有各级医生分析意见。
(3) 确定项目记分： 例如上述七项总分可定为100分。据以评定每份病史的分数。
(4) 划控制图： 例如抽查一个月病史，通过计算，求出中心线与范围线，据以控制每个医生的病史体检质量。系统的可靠性 由一组单元构成的体系、设备或程序，称为一个系统。例如急救站主要是由救护车、司机、值班护士和医生组成的系统。系统保持其正常功能 （不发生故障）的概率，称为系统的可靠性。
一个系统，按其组成单元之间的关系，可分为三类：
串联系统——其中任何一个单元发生故障均使整个系统不能正常工作。n个单元之间的关系如下图所示。

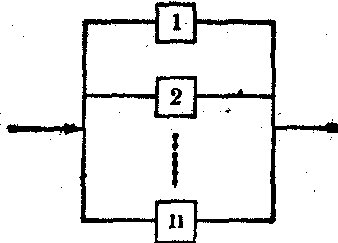
并联系统——只要有一个单元保持正常功能，就能使整个系统照常工作。各单元之间的关系如下图所示。

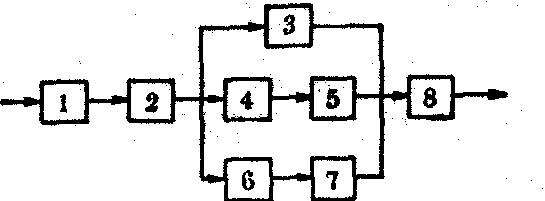
混合系统——由一些串、并联系统复合而成。这是实际上常见的。各单元之间的关系如下图所示。

用P表示系统保持正常功能的概率，即可靠性；P1表示第一个单元不发生故障的概率，q₁＝1-P1串联系统的可靠性为

P=P₁×P₂×……×Pn (1)

并联系统的可靠性为

P=1-q₁×q₂×……×q_n (2)

如果某个急救站系统为一个简单的串联系统。今设救护车暂时发生故障、司机缺勤、护士与医生缺勤的概率(q1)分别为0.05，则此系统的可靠性为

P=P1×P₂×P₃×P₄＝(1-0.05)(1-0.05)(1-0.06)(1-0.05)=.8145

即此急救站系统正常运行的机会为81%
如果该急救站系统为一个并联系统有两套人员和救护车，故障发生率各为0.05，司机缺勤率为0.20则本日该站系统正常运行的可靠性为

P=1-0.05×0.20=0.99