协方差分析

分析实验数据的一类统计方法。设y_ij(i=1,2，…r,j=1,2，…c)是按单因子Ar个水平重复c次的数据，还知道有一个可控变量或向量x_ij对数据y_ij有影响。如果y_ij不受因素Ar的影响，而仅仅受x_ij的影响，就可当作一个回归问题来处理；现在要将二者合并起来处理，则需要协方差分析以判断x_ij对y_ij是否有显著影响。变量x_ij称为共变量或共边向量。实质是方差分析和回归分析的合并。常被应用于测验分数统计中。

协方差分析analysis of covariance

亦称共变数分析。是将直线回归与方差分析结合起来使用分析实验数据的方法。当进行统计假设检验时，如随机变量y的变动与另一随机变量x的变动有关，即y与x存在回归关系，在引入另一变量x后，再进行假设检验，即可有效地缩小y的变异，从而提高假设检验的精确度。常用者有完全随机、随机区组、拉丁方多元等协方差分析。

协方差分析

协方差分析是把线性回归与方差分析结合起来，检验两个或多个修正均数间有无差别的方法。例如在营养研究中，不考虑动物食量的差别，直接用方差分析来比较不同饲料组动物所增体重的均数，以评价不同饲料的营养价值是不够恰当的。因为动物体重的增加，除与食物的营养价值有关外，还与各组动物的食量有关。而动物食量的多少又往往未加控制。若用直线回归的方法找出食量与所增体重的关系，求得当食量化为相等时（即扣除食量的影响），各饲料组动物所增体重的修正均数，然后再用方差分析检验各修正均数间有无差别，这才比较合理。又如比较各种职业人群的血压时，应把年龄化为相等，再作比较。这类问题，根据实验设计的不同，有完全随机设计、配伍组设计、拉丁方设计和析因设计等资料的协方差分析，其基本思想相同。本条目仅介绍前面两种，并以二元线性回归为例说明多元协方差分析。
应用协方差分析的条件是：
❶理论上要求各组资料（样本）都来自方差相同的正态总体；
❷各组的总体直线回归系数βi相等，且都不为0。因此，资料用协方差分析前须先进行方差齐性检验和回归系数的假设检验，若符合上述两个条件，或经变量变换后符合上述条件，方可进行协方差分析，否则不宜用此法。
完全随机（或配伍组）设计资料的协方差分析 方法步骤如下：
(1) 计算各变量值之和∑X、∑Y，平方和∑X₂、∑Y₂，及积和∑XY，如表1或表3下半部。
(2) 计算总变异的离均差平方和、积和及自由度，按式(1)～(3)。

式中∑X、∑Y、∑XY是各组X、Y、XY的总和，N为总例数，v为自由度。lXY/v称为协方差，它是两变量联合变异的度量。
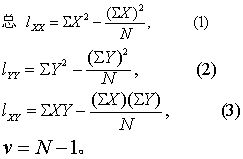
(3) 计算各处理组（或配伍组）间的离均差平方和、积和及自由度，按式(4)～(6)。

式中∑X_i或∑Y_i为第i组变量值X或Y的和，ni为第i组的例数，k为组数，其他符号意义同前。
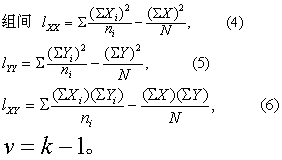
(4) 将上述第(2)、(3)步的计算结果列入协方差分析表，如表2或表4左侧部分。由总变异的离均差平方和、积和及自由度减处理组（或配伍组）间相应各数，得组内（或误差）的离均差平方和、积和及自由度。
(5) 求回归的剩余平方和∑(Y-Ŷ)²及自由度v。 列入协方差分析表，如表2或表4右侧部分。表2“剩余”部分：平方和栏中，总的及组内（或误差）的数字分别按式(7)计算，

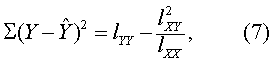
总的减组内的即为修正均数间的剩余平方和。自由度栏中，总的及组内数字分别为左侧相应部分的自由度减1，如总的v=39-1=38，组内的v=38-1=37，总的减组内的即为修正均数间的自由度v=38-37=1。
在配伍组设计中，总变异扣除了配伍组间的变异即处理组间的变异与误差的变异，因此，“组间+误差”的剩余与完全随机设计中的总剩余相当，如表4剩余部分的“饲料+误差”行与表2剩余部分的总变异行相当。
(6)分别求修正均数间及组内的剩余均方MS （即剩余平方和除以自由度之商）。再按式(8)求F值。

(7)用式(8)中分子、分母两均方的自由度查F界值表得P值，按所取检验水准作出推断结论。若修正均数间有差别，必要时再作两两比较。
(8)求各修正均数。先按式(9)计算公共回归系数bc，再按式(10)计算各修正均数'i。

式中i、 _i分别为第i组变量X、 Y的均数，为总均数。
(9)修正均数间的两两比较。见条目“多个样本均数间两两比较”，用q检验，唯统计量q值的计算按式(11),

式中'A、'B为任两修正均数， 分母为其差的标准误，sY2·X为组内剩余方差，n0为每组平均例数，α为对比的两均数间包含的组数，意义详见条目“多个样本均数间两两比较”。求得q值后，按“剩余”中组内自由度及α查q界值表得P值，按所取检验水准作出推断结论。
例1 表1中男性运动员和大学生的平均肺活量分别为4399cm³及3667.5cm3，经假设检验有差别。但肺活量的大小与身高有关，一般运动员的身高高于大学生。为进一步分析肺活量的差异是否由于体育锻炼所致，试进行协方差分析。

表1 某地20岁男性运动员及大学生的身高(cm) X与肺活量(cm⁸) Y

	运 动 员		大 学 生		合 计
	X1	Y1	X2	Y2
	184.9 167.9 171.0 171.0 188.0 179.0 177.0 179.5 187.0 187.0 169.0 188.0 176.7 179.0 183.0 180.5 179.0 178.0 164.0 174.0	4300 3850 4100 4300 4800 4000 5400 4000 4800 4800 4500 4780 3700 5250 4250 4800 5000 3700 3600 4050	168.7 170.8 165.0 169.7 171.5 166.5 165.0 165.0 173.0 169.0 173.8 174.0 170.5 176.0 169.5 176.3 163.0 172.5 177.0 173.0	3450 4100 3800 3300 3450 3250 3600 3200 3950 4000 4150 3450 3250 4100 3650 3950 3500 3900 3450 3850
n	20		20		40
∑X	3563.5		3409.8		6973.3
∑Y		87980		73350	161330
∑X2	635867.81		581653.8		1217521.61
∑Y2		392398400		270917500	663315900
∑XY	15710815		12515760		28226575
	178.175		170.49		174.3325
		4399		3667.5	4033.25

H₀:两总体肺活量的修正均数相等，H₁:两总体肺活量的修正均数不等。
a=0.05。
初步计算结果见表1下半部。按式(1)～(6)得：

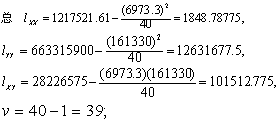
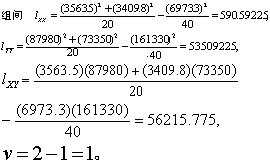
表2 表1资料的协方差分析

变异来源	v	离均差平方和及积和			剩 余
		lXX	lXY	lYY	v	∑(Y-Ŷ)2	MS
总 组 间	39 1	1848.78775 590.59225	101512.775 56215.775	12631677.5 5350922.5	38	7057839.46
组 内	38	1258.19550	45297.000	7280755.0	37	5649992.365	152702.4964
修正均数间					1	1407847.095	1407847.095

按式(7)、(8)求剩余平方和、自由度、均方(结果列入表2右侧部分)及F值，计算如下：

查F界值表得P<0.01，按a=0.05水准拒绝H₀ ，接受H₁，可以认为两组肺活量均数在消除身高因素的影响后有差别，运动员的肺活量大于大学生。
按式(9)、(10)求两组肺活量的修正均数为：

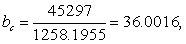
′运=4399-36.0016(178.175-174.3325)=4260.66,′学=3667.5-36.0016(170.49-174.3325)=3805.84。
例2 研究核黄素缺乏对蛋白质利用的影响，按配伍组设计将36只大白鼠分成12个配伍组，再将每个配伍组的3只大白鼠随机分入三个饲料组。第一组喂以缺乏核黄素饲料； 第二组喂以含核黄素饲料，限制食量使与第一组食量相近； 第三组喂以含核黄素饲料，但不限制食量。三组大白鼠之进食量与所增体重见表3，试比较三组白鼠所增体重的修正均数间有无差别。

表3 三组大白鼠之进食量(g) X与所增体重 (g)Y

H₀:所增体重的三个总体修正均数相等，
H₁:三个总体修正均数不等或不全相等。
α=0.05。
初步计算结果见表3下半部。按式(1)～(6)得

表4 表3资料的协方差分析

变异来源	v	离均差平方和及积和			剩 余
		lXX	lXY	lYY	v	∑(Y-Ŷ)2	MS
总 配伍组间 饲 料 间	35 11 2	508150.076 87586.703 383620.127	187349.144 36638.307 135607.964	75786.356 19089.116 48297.627
误 差 饲料+误差	22 24	36943.246 420563.373	15102.873 150710.837	8399.613 56697.240	21 23	2225.36 2689.31	105.97
修正均数间					2	463.95	231.98

按式(7)、(8)求剩余平方和、自由度、均方(结果列入表4右侧部分)及F值计算如下：

查F界值表得P>0.05，按α=0.05水准不拒绝H₀，虽然三组的所增体重均数(37.1,45.7,118.7)看起来相差较大，但经检验不能认为三组所增体重的修正均数间有差别。三个修正均数按式(9)、(10)为：

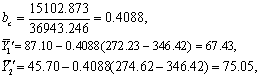
'3=118.74-0.4088(492.40-346.42)=59.06。
多元协方差分析 若实验中需要将两个或两个以上的因素都化为相等，然后分析某变量修正均数的差别，而这些因素与某变量呈线性相关，那么可进行多元协方差分析。如欲将各组动物的食量与原始体重都化为相等，然后比较各组所增体重的修正均数间有无差别，则先用多元线性回归的方法，将食量、原始体重与所增体重的关系找出来，求出当食量、原始体重化为相等时，各饲料组所增体重的修正均数，然后用方差分析检验各修正均数间有无差别。现以二元回归为例说明其计算步骤如下：
(1)计算各变量值的总和、平方和及积和，如表5。
(2) 计算总变异的离均差平方和及积和，按式 (1)～(3)；计算组间离均差平方和及积和，按式(4)～(6)；两相应部分相减，得组内离均差平方和及积和。如表6。总的自由度为总例数减1，组间自由度为组数减1，组内自由度为二者之差。
(3)计算总变异的偏回归系数b₁、b₂及决定系数R₂，按式(12)～(14)；同法计算组内的b₁、b₂及R₂。

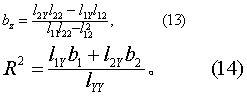
(4) 求剩余平方和∑(Y-Ŷ)²及自由度v。 列多元协方差分析表如表7右侧部分。其中总平方和及组内平方和分别按式(15)计算，
∑(Y-Ŷ)²＝(1-R²)lYY。 (15)
自由度为左侧相应部分的自由度减2；剩余平方和中总的减组内的即得修正均数间剩余平方和，自由度亦为相应两自由度之差。
(5) 分别求修正均数间及组内的剩余均方MS （即剩余平方和除以自由度之商）。再按式(8)求F值，查F界值表得P值按所取检验水准作出推断结论。
(6) 按式 (16) 求各修正均数′i, 必要时作两两比较。

式中b₁及b₂为组内偏回归系数。
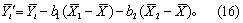
例3 试根据表5列出的初步计算结果，将食量和原始体重都化为相等，再比较三组大白鼠所增体重的修正均数。

表5 三组大白鼠的食量、原始体重与增重的初步计算结果

饲料组	动物数	食 量		原始体重		所增体重
		∑X1	∑X21	∑X2	∑X22	∑Y	∑Y2
第一组 第二组 第三组	12 12 12	3266.8 3295.5 5908.8	914414.52 928816.85 2985150.24	1012.2 1061.5 1072.0	86395.94 94806.75 97532.50	445.2 548.4 1424.9	21204.72 31065.56 185992.25
合 计	36	12471.1	4828381.61	3145.7	278735.19	2418.5	238262.53
		∑X1X2		∑X1Y		∑X2Y
第一组 第二组 第三组		277830.08 293532.20 538185.40		130517.23 160610.30 734037.04		37652.71 48938.60 133346.45
合 计		1109547.68		1025164.57		219937.76

H₀:三个总体修正均数相等，
H₁:三个总体修正均数不等或不全相等。
a=0.05。

表6 组间与组内之离均差平方和及积和[按式(1)～(6)]

	离 均 差 平 方 和			离 均 差 积 和
	l11	l22	lYY	l12	l1Y	l2Y
总 组 间 组 内	508150.08 383620.13 124529.95	3862.18 169.91 3692.27	75786.36 48297.63 27488.73	19816.03 5190.17 14625.86	187349.14 135607.96 51741.18	8607.886 2024.363 6583.523

按式(12)～(15):

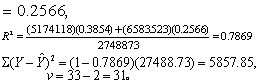
表7 表5资料的协方差分析

变异来源	v	lYY	R2	剩 余
				v	∑(Y-Ŷ)2	MS
总 组 间	35 2	75786.36 48297.63	0.9188	33	6153.85
组 内	33	27488.73	0.7869	31	5857.85	188.96
修正均数间				2	296.00	148.00

今修正均数间的剩余均方小于组内的剩余均方，则按式(8)计算的F值必小于1，故知P>0.05，按α=0.05水准不拒绝H₀，说明将食量及初重化为相等后，不能认为三组所增体重的修正均数间有差别。按表5资料及式(16)计算三个修正均数为：'1=37.10-0.3854(272.23-346.42)-0.2566(84.35-87.38)=66.47,
'2= 45.70-0.3854(274.62-346.42)-0.2566(88.46-87.38)=73.09,
'3=118.74-0.3854(492.40-346.42)-0.2566(89.33-87.38)=61.98。

协方差分析covariance analysis

协方差分析模型为自变量既有属性变量，也有数量变量的模型，即：

y=xβ+zγ+ε (1)

其中x为属性自变量，取值为0或1，称xβ为方差分析部分；z为数量自变量，即可连续取值，称zγ为回归分析部分。模型(1)可改写为：

y*=xβ+ε

其中y*=y-zγ。因y*中含未知参数γ，不能
将y*看做观测值向量。处理的方法是在y^*中以γ的一个适当的估计量γ代替γ，从而得到一个以*=y-z为观测值向量的方差分析模型。
*=xβ+u (2)
事实上，可从(1)消去方差分析部分后导出的模型

Py=Pzγ+Pε

估计出，其中P=I-x(x′x)^-1x′。于是

γ=(z′Pz)^-1z′Py

可以看出，对模型(1)中方差分析部分的统计分析，可通过纯方差分析模型(2)进行。由于已经消去zγ项，可直接应用方差分析中的现成结果，这就带来了很大方便。
由于在对(2)作方差分析时必然出现如z′Py这样的量的计算，似与z与y的样本协方差相近，故称之为协方差分析。

协方差分析covariance analysis

回归分析与方差分析相结合的一种统计分析方法。它与方差分析的不同之处在于：方差分析的各因素水平可以根据需要和实际情况人为地加以控制，而在协方差分析中，某些因素的水平是不能控制或难以控制的。如在考察不同教学方法对学生学习成绩有无显著性影响的过程中，如果只考虑教学方法对学生学习成绩的作用，而不考虑学生的智力水平和学习基础这两个不能精确控制的因素对学生学习成绩的影响，将会影响判断的准确性。协方差分析可以消除这种不可控因素的影响，提高分析的精度。教学方法是可以人为控制的因素，称为方差因素，而学生的智力和学习基础是不能精确控制的因素，称为协变量。协方差分析的基本方法是先对每一水平下的试验结果进行回归分析，求出扣除协变量以后的残值，再将各水平试验下对应的残值进行方差分析。协方差分析适合于完全随机化设计资料、随机化区组设计资料、拉丁方资料等。

协方差分析analysis of covariance

通过分析和分离协变量对因变量的影响效应，揭示实验处理效应的多元分析方法。用ANCOVA表示。多用于对实验数据处理的统计控制，是方差分析和回归分析的综合，可用于不同的实验设计。当研究者知道某些协变量(如研究学习时间对学习绩效的影响时，学生原有知识结构、智力、学习兴趣等为协变量)会对因变量产生影响，却不能控制或不感兴趣时，可在实验处理前对协变量予以观测，然后运用协方差分析来揭示协变量的影响效应。协变量是可测的，并具有一定变化范围，实际分析中通过回归分析分离其变异，然后通过方差分析探讨研究者所关心的自变量的影响效应。当协变量与自变量之间存在交互作用时，分析的方法和过程将更加复杂。将协变量对因变量的影响从自变量影响效应中分离出来，可以进一步提高实验精确度和统计检验灵敏度。