协方差

设(ξ₁,ξ₂)是二维随机变量，如果其分量与各自的数学期望之差乘积的数学期望存在，则称它为随机向量(ξ₁,ξ₂)的协方差，或二阶混合中心矩，记为σ^ξ₁ξ₂，或cov(ξ₁,ξ₂)，即有

一般地，设(ξ₁……ξ_n)是n维随机向量，如果数学期望E([ξ_i—E(ξ_i)][ξ_k—E(ξ_k)])存在，则称它为随机变量ξ_i与ξ_k的协方差，即有

其中i≠k(i,k=1,2，…，n),i=k时，有

协方差σ^ξ_iξ_k是用来刻画随机变量与线性相关程度的一个数字特征，它是方差概念对于两个随机变量情形的推广。常被应用于测验分数统计中。

协方差covariance

旧称互变量。两组变数离均差的乘积和除以自由度所得的商。以COV表示。

式中的n为两变数资料的成对数。

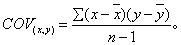
协方差Covariance

设随机变量ζ₁、ζ₂的数学期望分别为Eζ₁和Eζ₂，则称E[(ζ₁-Eζ₁)(ζ₂-Eζ₂)]为ζ₁、ζ₂的协方差。它是反映随机变量之间线性相关程度的数字特征。在测量中，是描述两观测量线性相关程度的一种指标。