动态规划dynamic programme

研究多阶段决策过程最优化的一种数学方法。常用来解决一些有时间或空间变动因素的经济问题。具体方法是：将一个复杂的多阶段决策问题划分为若干个阶段，在每一阶段中，列举出可能的若干个决策；在每一阶段选择一个决策，并按阶段先后次序排列起来、得到一个决策序列，这一序列称为策略；建立评价函数来描述每一阶段中诸决策的瞬时效果，然后建立最优评价函数来衡量最优决策序列的总效果。根据动态规划最优化原理，动态规划求解，要从最后阶段开始，逐段由后向前推移，直至初始阶段寻找出最优解。即首先依据评价函数确定最后阶段的最优决策，然后利用这一结果与评价函数确定倒数第二阶段的最优策略，依此递推进行，在初始阶段得到的最优策略，就是动态规划的最优解。动态规划因研究的决策过程不同，可分为离散确定型、离散随机型、连续确定型、连续随机型等4种类型。

动态规划

见“规划论”。

动态规划Dynamic Programming

求解多阶段序贯决策问题的最优化方法。多阶段序贯决策问题是一种复杂的决策问题，它在时间（或是由解题方便而规定的其他因素）上分为若干阶段，其中每阶段都需做出决策，而困难之处在于前面做出的决策将会影响后面的决策。求解一个动态规划问题，所遵循的方法来自于“最优性原理”，即一系列的决策如果是最优的话，那么它其中任何一个子决策（若干相连的决策）也是最优的。这从直观上来说是明显的，因为如果子决策不是最优的话，将可以找到一个更好的子决策，这将使得总的一系列决策更好，从这条原理可以得出动态规划问题的求解方法，由后向前，逐步递推。为了讲述解法，先引进一些记号：设阶段变量k(1≤k≤n)表示决策阶段；状态变量S_k表示第k阶段的状态，这由初始状态及已作出的决策而定；决策变量x_k(S_k)表示在第k阶段时处于S _k状态下所做的决策；损益变量d[S_k,X_k(S_k)]表示在S_k状态下作决策x_k(S_k)所带来的损益；f_k(S_k)处于S_k状态下的最优决策序列。有了这些变量，根据最优性原理，动态规划的模型可以表达为：

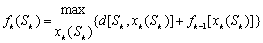
这表示第K阶段的最优决策序列是由前一阶段(注：一般标号以最靠近目标的标为1阶段，稍远的标为第2阶段，以此类推)所做的最优决策序列与本阶段所做决策的损益之和的最大值。
例：最短路问题，已知A地到D地的各条道路及长度如图11-6，求从A到D如何走最近。

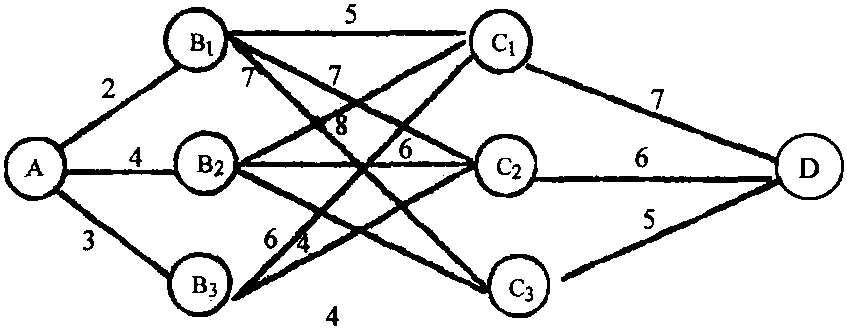
图11-6

在这个问题中，阶段明显为A→B→C→D三个阶段，各C是第1阶段，各B是第2阶段，A为第三阶段，状态变量即各地点，决策变量即各道路，损益变量即各道路之长，最终的决策序列即一系列道路，而目标为路长之和最短，求解如下：
从图中直接可以看出：
f₁(C₁)=7(x₁^*＝C₁→D)
f₁(C₂)=6(x₁^*＝C₂→D)
f₁(C₃)=6(x₁^*＝C₃→D)
(注：变量加星号表示最优解)
对于B₁:
f₂(B₁)=min{d[x₁(B₁,B₁)]+f₁[x₂(B₁)]}
＝min{d(C₁,B₁)+f₁(C₁),d(C₂,B₁)
+f₁(C₂),d(C₃,B₁)+f₁(C₃)}
=min{5+7,7+6,7+5}
＝12(x₂^*＝B₁→C₁或x₂^*＝B₁→C₃)
同理可求得B₂,B₃:

f₂(B₂)=7(x₂^*＝B₂→C₃)
f₃(B₃)=9(x₂^*＝B₃→C₂)

对于A:
f₁(A)=min{d(A₁B₁)+f₂(B₁),d(A₁B₂)+
f₂(B₂),d(A₁B₃)+f₂(B₃)}
=min{2+12,7+4,3+9}
=11 (x₁^*＝A→B₂)
因此，最短路长为11，走法为（将各最优解串联即可）,A→B₂→C₃→D。

动态规划

研究多阶段决策过程最优化问题的一种方法，是运筹学的一个分支科目。动态起源于本世纪40年代后期关于水利资源、数理统计的序列分析以及库存论的研究。1951年，美国数学家贝尔曼提出了“最优化原理”，他把解决最优化问题的方法称为“动态规划”。1957年，他出版了《动态规划》一书，这是动态规划问题的第一本专著。最优化原理认为，在多步决策过程中，最优策略序列有如下性质：“从给定的初始状态出发，经第一步决策所获得的最优策略序列，对所有后续各步来说也是最优的。”根据这个原理形成的基本方法是：从多阶段决策序列的终点开始，按逆序逐段向始点推进，通过递推使过程不断转移，最终获得目标函数的最优值。如报刊发行路线从A城到B城，中间有若干城镇与通道，要求出从A到B的最短投递路程(最短路程概念可以理解为距离、工序、时间、费用等极小值的度量)。首先，从终点向始点逆向地将运输线网络分成若干阶段或过程，然后确定每个阶段的状态变量，它可以是一个数或一组数，如距离数值。继之，从每个阶段的每个始点出发，选择到终点的决策变量或决策变量的集合。由于前一个阶段的最优决策序列也是后一阶段的最优决策序列，根据最优原理的递推关系最终求出AB之间的最短路程或最小开支、最短时间。递推求解由建立递推方程进行运算。动态规划与一般规划的不同是：在模型上具有明显的阶段性和序列性；在方法上是多步决策，通过递推关系使决策过程不断转移，这也是“动态”的含义。目前，在工程技术、经济管理、生产过程等方面都有广泛应用。在报刊发行系统、有线广播线路设计等，可以用动态规划求解最优线路、最优时间、最优费用等问题。

动态规划

一种能够解决多阶段决策过程最优化问题的方法。在经济学中常用来解决 一些含有时间和空间变动因素的经济问题。它通常是通过建立数学模型来求解那些资源一定、在时间上和空间上相互关联的经济活动的最大收益。根据决策变量是连续的还是离散的，动态规划所建立的数学模型相应地分为连续性数学模型和离散性数学模型，根据决策变量是确定性的还是随机性的，动态规划的数学模型相应地分为确定性动态规划模型和随机性动态规划模型。其中，以确定性动态规划模型为主。求解动态规划模型的常用方法有分析法、数值求解法、动态规划表等方法动态规划方法是美国数学家贝尔曼(R.Bellman) 等人于1951年最先提出的。这一方法在工程技术、管理、经济、工业生产、军事以及现代工程控制等方面都有广泛的应用。