利用配对原理计数Liyong peidui yuanli jishu

把要计数的集合的元素与另一个已知或较易计算的集合的元素之间建立对应关系， 由后一集合的元素个数推知前一集合的元素个数。这就是配对原理。
例1（第二届华罗庚金杯赛决赛第二试）:有50名学生参加联欢会， 第一个到会的女生同全部男生握过手；第二个到会的女生只差一个男生没握过手，第三个到会的女生只差2个男生没握过手，如此等等，最后一个到会的女生同7个男生握过手，问这50名同学中有多少男生？
解：根据配对原理，可知男生比女生多6人，因此，男生有28人， 女生有22人。
例2:如下图示的立体图形叫做二十面体，它有20个面， 那么， 它有多少条棱？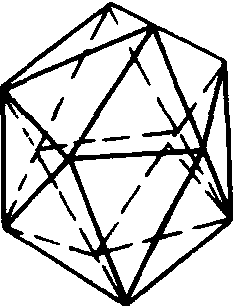
解： 注意到每个面由三条棱围成，因此，可以建立面与棱之间的对应关系， 使得每个面对应包围它的3条棱，此外，每条棱又是两个相邻面的公共边，这就是说，在上述对应中，每条棱都出现过2次，于是可得2×棱数=3×面数=60，故正二十面体有30条棱。
例3:设乒乓球比赛有1 992名选手参加，比赛采用淘汰制， 最后决出冠军1名， 问共须安排多少场比赛。
解：由于是淘汰赛，每场比赛将淘汰1名选手，比赛到最后， 只有冠军1人未被淘汰， 被淘汰的选手有1 991人， 故共须安排1 991场比赛。
采用配对原理计数，要点在于正确选择对应关系，有的情况下，所得对应关系不是1对1的，这时需要计算隐含于对应关系内部的数量关系，如例2就是如此。