分部积分法
分部积分法fenbujifenfa
设u(x),vυ(x)可导,且不定积分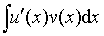 存在,则
存在,则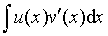 也存在,且
也存在,且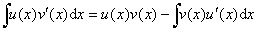 即
即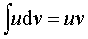
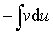 这个公式称为分部积分公式. 若求
这个公式称为分部积分公式. 若求
| ⨜u(x)v′(x)dx |
| ⨜v(x)u′(x)dx |
用分部积分法求不定积分,一般分为四步:
❶选定u,v,将所求积分
| ⨜uv′dx |
| ⨜udv. |
❷代公式,即
| ⨜udv=uv-⨜udv. |
❸将所得的新积分
| ⨜udv |
| ⨜uu′dx, |
❹计算
| ⨜uu′dx. |
使用分部积分法的关键在于恰当地选定被积表达式中的u,使
| ⨜vdv |
| ⨜udv |
❶对于积分
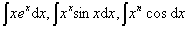 等,可取“=x2,余下的部分作dv,以便利用分部积分法降低x n的次数.
等,可取“=x2,余下的部分作dv,以便利用分部积分法降低x n的次数.❷ 对于积分
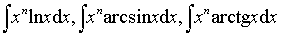 等,可将其中的超越函数取作u,v=xmdx,以便用分都积分法将超越函数化为代数函数.
等,可将其中的超越函数取作u,v=xmdx,以便用分都积分法将超越函数化为代数函数.❸ 对于积分
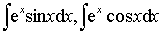 等,须多次使用分部积分法.每次选作u的函数,一般说来必须是同类函数,比如两次都选ex作u,或两次都选三角函数作u.
等,须多次使用分部积分法.每次选作u的函数,一般说来必须是同类函数,比如两次都选ex作u,或两次都选三角函数作u.例1 求
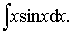
解 设u =x,du =sinxdx,则v =-cosx.
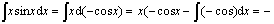
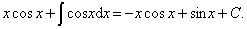
例2 求
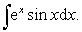
解 设u =sinx于是
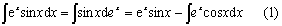
再设u =cosx,于是
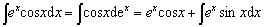
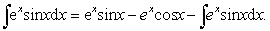
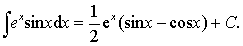
☚ 不定积分的第二换元积分法 有理函数的不定积分 ☛
分部积分法
integration by parts
- 卜颜帖木儿是什么意思
- 卜食是什么意思
- 卜鲁斯是什么意思
- 卜鲁罕是什么意思
- 卜鲁罕皇后(伯岳吾氏)是什么意思
- 卜龟儿卦是什么意思
- 卝是什么意思
- 卞是什么意思
- 卞三元是什么意思
- 卞之琳是什么意思
- 卞之琳是什么意思
- 卞之琳是什么意思
- 卞之琳是什么意思
- 卞之琳与诗艺术是什么意思
- 卞仪文是什么意思
- 卞兰是什么意思
- 卞后(卞太后)是什么意思
- 卞和是什么意思
- 卞和献玉是什么意思
- 卞塔海是什么意思
- 卞壸是什么意思
- 卞大亨是什么意思
- 卞太后是什么意思
- 卞奭年是什么意思
- 卞季良是什么意思
- 卞宗彬是什么意思
- 卞宝是什么意思
- 卞寿孙是什么意思
- 卞庄子是什么意思
- 卞庄子刺虎是什么意思
- 卞彭是什么意思
- 卞思义是什么意思
- 卞急是什么意思
- 卞敬德是什么意思
- 卞杏英是什么意思
- 卞氏王夫人墓誌是什么意思
- 卞永誉是什么意思
- 卞璞是什么意思
- 卞田居是什么意思
- 卞祖武是什么意思
- 卞秀欣是什么意思
- 卞稚珊是什么意思
- 卞章五是什么意思
- 卞致璋是什么意思
- 卞荣鲁是什么意思
- 卞荣鲁是什么意思
- 卞荫昌是什么意思
- 卞葆芝是什么意思
- 卞随是什么意思
- 卞鸿儒是什么意思
- 卞鹤圭是什么意思
- 卞鼒是什么意思
- 卟是什么意思
- 卟吩姆钠是什么意思
- 卟啉代谢是什么意思
- 卟啉症病是什么意思
- 占是什么意思
- 占是什么意思
- 占是什么意思
- 占是什么意思