凸集
凸集tuji
一类特殊的点集.若对于点集M中任意两点A和B,线段AB上的每一点都属于点集M,则M就叫做凸集.
根据凸集的定义可知,平面、半平面(包括开半平面和闭半平面)、带形区域、直线、射线和线段等都是凸集.
还可以证明,凸多边形区域、圆域、椭圆域等都是凸集.
另外约定,空集Φ和只含一个点的点集都是凸集.
若M1,M2是任意两个凸集,则它们的交集M=M1∩M2也是凸集.这个结论也可以推广到任意多个凸集的情况,即若M1,M2,…,Mn是任意n个凸集,则它们的交集也是凸集.
M=M1∩M2∩…∩Mn
凸集的概念主要用于覆盖问题.例如,当两个点集M,N的点之间可以建立起一一对应,并且对于点集M中的任意两点A,B和点集N中对应的两点A′B′,有AB/A′B′=k(k为正常数)时,就称点集M与N为相似点集.若点集M与N相似,M的直径大于N的直径,并且M是凸集,则点集M能覆盖点集N.
☚ 覆盖 数集 ☛
- 没年年是什么意思
- 没年纪是什么意思
- 没幸是什么意思
- 没庐·赤洁莫赞是什么意思
- 没底是什么意思
- 没底儿是什么意思
- 没底儿跟头是什么意思
- 没底子是什么意思
- 没底数是什么意思
- 没底棺材是什么意思
- 没底的吊桶是什么意思
- 没底的斤斗是什么意思
- 没底矩是什么意思
- 没底竹篮打水,无根铁树生花是什么意思
- 没底竹篮汲水是什么意思
- 没底货是什么意思
- 没店三是什么意思
- 没开交是什么意思
- 没开怀是什么意思
- 没开怀儿是什么意思
- 没开扎是什么意思
- 没开晴是什么意思
- 没开没解是什么意思
- 没开眼是什么意思
- 没开窍是什么意思
- 没开解是什么意思
- 没开赚是什么意思
- 没开锣就坍台是什么意思
- 没弄到点子上是什么意思
- 没弈干是什么意思
- 没张倒置是什么意思
- 没张倒致是什么意思
- 没张没致是什么意思
- 没张置是什么意思
- 没张致是什么意思
- 没弦的琵琶是什么意思
- 没弦的琵琶——从哪儿弹起是什么意思
- 没弦的琵琶——从哪儿弹(谈)起是什么意思
- 没弦的琵琶——空弹(谈)是什么意思
- 没弹剥是什么意思
- 没弹挣[t‘
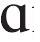
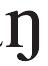 tse
tse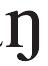 ]是什么意思
]是什么意思 - 没当家花花的是什么意思
- 没形没影是什么意思
- 没影是什么意思
- 没影了是什么意思
- 没影儿是什么意思
- 没影儿的事是什么意思
- 没影子是什么意思
- 没影子的事是什么意思
- 没影子的话是什么意思
- 没影的是什么意思
- 没影的事是什么意思
- 没影的事儿是什么意思
- 没得是什么意思
- 没得一个好的是什么意思
- 没得主是什么意思
- 没得了是什么意思
- 没得事是什么意思
- 没得二行是什么意思
- 没得你呢法儿是什么意思