关系推理

前提和结论都是关系判断的一种演绎推理。关系推理分为直接关系推理和间接关系推理两种。直接关系推理是从一个关系判断推出另一个关系判断的关系推理，如：“李白和杜甫同时代，所以，杜甫和李白同时代。”间接关系推理是从两个关系判断推出一个关系判断的关系推理，如：“孔子早于孟子，孟子早于荀子，所以，孔子早于荀子。”根据关系的逻辑特性，直接关系推理分对称性关系推理和反对称性关系推理两种； 间接关系推理分为传递性关系推理和反传递天系推理两种。对称性关系推理依据对称性关系，以一个对称性关系判断作前提，以另一个对称性关系判断作结论，如：“小王和小张是同学； 所以，小张和小王是同学。”其公式是： aRb; 所以，bRa。反对称性关系推理依据反对称性关系，以一个关系判断作前提，以另一个关系判断作结论。如：“墨子早于庄子； 所以，庄子不早于墨子。”其公式为： aRb，所以，b非Ra。传递性关系推理依据传递性关系，以两个关系判断作前提，以另一个关系判断作结论。如：“孔子早于孟子，孟子早于荀子； 所以，孔子早于荀子。”其公式为： aRb,bRC；所以，aRC。这种推理在数学中应用较广。反传递性关系推理依据反传递性关系，以两个关系判断作前提，以另一个关系判断作结论。如：“小张比小王高一年级，小王比小李高一年级； 所以，小张不比小李高一年级。”其公式为： aRb,bRC; 所以a非RC。

关系推理guanxi tuli

以对象间的关系判断作为前提和结论，根据关系的性质，由前提必然地推出结论的一种常见的演绎推理.关系推理可分为直接关系推理和间接关系推理.
直接关系推理是由一个关系判断，根据关系的性质，必然地推出关系判断的结论的推理.常见的直接关系推理有：
❶对称性关系推理 当给定的对象的关系R具有对称性(若aRb，则必有bRa)时，以下推理是正确的：

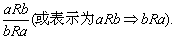
例如，AB∥CD∥CD∥AB是一个正确的关系推理(其中符号“∥”表示直线间平行关系).

❷严格反对称性关系推理 当给定的对象的关系R具有严格反对称性(若aRb，则必有ba)时，以下推理是正确的：

例如 2>1⇒1≯2.
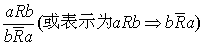
间接关系推理是由两个关系判断的前提，根据关系的性质，必然地推出一个关系判断的结论的推理.常见的间接关系推理有：
❶传递性关系推理 当给定的对象的关系R具有传递性(若aRb,bRc，则必有aRc)时，以下推理是正确的：

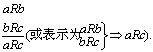
例如，

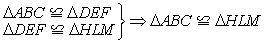
(其中符号“≌”表示三角形全等关系).

❷反传递性关系推理 当给定的对象的关系R具有反传递性(若aRb, bRc，则必有ac)时，以下推理是正确的：

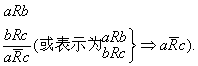
例如， 平面π上

是一个正确的推理.
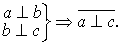
此外，中学数学中还有一些利用关系的性质进行的关系推理.例如，在实数范围内，可以作出如下一些关系推理：(a=b)⇒(a²＝b²);(a=b)⇒(a±c=b±c);(a≥b)⇒(a-b≥0);(a>b)并且(a=c)⇒(c>b)等等.这些都是正确的推理.

---

关系推理guanxi tuili

演绎推理之一。前提中至少有一个关系判断的推理。关系推理可分为纯关系推理和混合关系推理。
纯关系推理是前提和结论都是关系判断的关系推理。根据关系的对称性和传递性进行的关系推理主要有下列4种形式：

推理名称	推理形式
对称性关系推理	aRb, 所以， bRa
反对称性关系推理	aRb, 所以， bRa
传递性关系推理	aRb, bRc, 所以， aRc
反传递性关系推理	aRb, bRc, 所以， aRc

混合关系推理是其中一个前提是两项关系判断，另一个前提是性质判断，结论是两项关系判断的关系推理。亦称关系三段论。如所有a与b有R关系，凡c是a，所以，凡c与b有R关系。混合关系推理的规则是：
❶媒介概念（两前提中都包含的概念）在前提中至少周延一次。
❷在前提中不周延的概念在结论中不得周延。
❸前提中的性质判断必须是肯定的。
❹若前提中关系判断是肯定的，则结论也是肯定的；若前提中的关系判断是否定的，则结论也是否定的。
❺若关系R不是对称的，则在前提中作为关系者前项（或后项），在结论中也必须作关系者前项（或后项）。

关系推理

relation inference