二次曲线的不变量erci quxian de bubianliang

如果二次曲线的方程Ax²+Bxy+Cy²+Dx+Ey+F=0经过任意坐标变换后得到一个新方程A'x²+B'xy+C'y²+D'x+E'y+F'=0，由系数A,B,C,D,E,F所组成的一个函数f，若和由对应系数A′,B′,C′,D′,E′,F′所组成的相同的这个函数的值总是相等，即在不同的直角坐标系下总有f(A,B,C,D,E,F)=f(A′,B′,C′,D′,E′,F′)，那么称这个函数f为方程Ax²+Bxy+Cy²+Dx+Ey+F=0表示的二次曲线在直角坐标系下坐标变换的不变量.
定理 二次曲线Ax²+Bxy+Cy²+Dx+Ey+F=0在移轴和转轴变换下的不变量是H,△和I.其中 H=A+C=A′+C′

△=B²-4AC= B′²-4A′C′

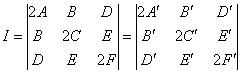
利用不变量可以检验移轴、转轴过程中，可能发生的计算错误，有时还可以用它们来简化转轴运算。用不变量来刻划曲线的几何特性，这在理论上有普遍意义.