中国古代数学
主要责任者: 郭书春
责任方式: 著
出版者: 商务印书馆
出版地: 北京
页码: 1-198
开本: 32
中图分类号: O112
装帧: 简
语种:中
定价:13.00
出版时间:1997-04
丛书多卷书否:是
丛书名:中国文化史知识丛书
丛书责任者:任继俞;汤一介,焦树安,张明华
丛书责任方式:主编;副主编
书目简介:本册工具书是中国文化史知识丛书之一，共收录54条词条。
被引频次：53

中国古代数学zhongguo gudai shuxue

中国古代数学源远流长，成果丰硕，其思想、方法与以古希腊为代表的西方数学迥异，地位独特，对世界数学的发展曾产生过重要影响.
从上古到东汉初期 (1世纪)是中国数学萌芽、积累并形成体系的时期. 半坡时代 (5～6千年前) 的刻划数学符号已初步形成了十进制系统. 殷商甲骨文(公元前13—前11世纪)中已有一至十及百、千、万的数名，有了三万这样的大数和简单的数字运算，还出现了 “规”“矩”二字，标志着这两种基本作图工具早已产生.
西周时，数学已成为贵族子弟必修的 “六艺”之一，称为 “九数”，可见内容广泛并已作了分类，成于周初的 《易经》 中已有初步的排列知识 (八卦，六十四卦).九数与八卦被历代学者认为是中国古代数学的重要源泉.
春秋时代，算筹已广泛应用. 据后来的记载，用算筹摆放数字有两种方式. 其1～9的摆法分别为

纵式

横式

多位数纵横相间（个位纵）.自然数与分数四则运算已完备. 不晚于战国，出现了河图和洛书，其中洛书是世界上最古老的三阶幻方.

春秋战国时期出现了理论几何学的雏形，得到了许多含义深刻的命题，如 “一尺之棰，日取其半，万世不竭” (《庄子》)，“穷，或 (即 “域”) 有前不容尺也” (《墨经》). 《考工纪》中有了角度概念的萌芽，天文测量中广泛使用了平行线，许多面积、体积和测量问题得到解决.
公元前2世纪的《算数书》标志着中国数学已初步形成体系，其体例和内容直接与后来的《九章算术》相通. 成于公元前2世纪的天文学著作《周髀》记载了分数运算、等差数列、矩的用法及一般形式的勾股定理.然而真正具有划时代意义的，是公元1世纪的《九章算术》 (简称 《九章》).
《九章》采用问题集形式，由问 （题目）、答 （答案）、术 （解法） 组成，有246问，202术，分为九类，其中出现了系统的分数算法、无理数概念及运算、正负数加减法则； 建立了完整的比例理论和算法； 详细记述了著名的 “盈不足术”；发展了一整套面积、体积算法及以勾股定理为中心的勾股恒等式、整勾股数公式及勾股测量； 给出了线性方程组的消元法； 处理了开平方、开立方及一元二次方程，成为后来高次方程数值解法的源头. 从形式、内容、方法和思想上，《九章》都极大地影响了后世的数学著作，而其中的分数算法、正负数、盈不足术、线性方程组解法、开方法在世界上长期领先，其盈不足术曾传入阿拉伯和欧洲.

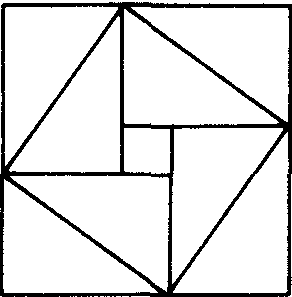
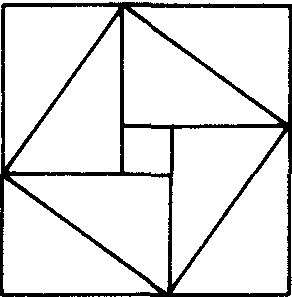
弦图

东汉初至五代末(10世纪)是中国数学持续发展与理论体系深化完善的时期. 3世纪，赵爽注《周髀》，用弦图给出勾股定理的一个精彩证明. 263年刘徽注《九章》，对古代数学的概念、成果、方法及思想进行了全面的整理和发展 (参见 “刘徽”). 他在研究球体积时所用的方法及引入的一牟合方盖 （两等径直交圆柱的公共部分） 导致后来祖暅概括出著名的“刘徽祖暅原理”(参见“祖冲之”).
南北朝时，祖冲之 （参见该条） 写成数学名著《缀术》 （已失传），并得到了精确到7位小数的圆周率值；《孙子算经》中的 “物不知数”问题及其解法，给出了著名的 “孙子定理” (通称 “中国剩余定理”)；《张邱建算经》给出最大公约数、最小公倍数、等差级数中一些重要的基本关系和公式，其 “百鸡问题”开中国古代不定方程理论研究的先河，并曾传入印度、阿拉伯及欧洲.
隋唐时期，由于天文学的推动，刘焯 (544—610)、张遂 （参见该条）先后创立了等间距和不等间距二次内插法. 受到印度正弦表的影响，张遂创制了正切表.唐初，王孝通在其《缉古算经》中对三次方程进行了广泛的研究，其方法高度体现了中国古代几何与代数紧密结合的特征.在这一时期，数学教育已制度化，包括机构、教师、学生、待遇、学制、考试、教科书等都有明确规定.同时，中国数学对朝鲜、日本产生了巨大影响，并与印度的数学进行了交流.许多数学成果由中国传入印度后，又经阿拉伯传入欧洲，对世界数学发展起到了很大的作用.
宋元时代(10—13世纪)是中国古代数学的高峰期，数学在内容、方法与形式上都发生了飞跃.在内容上，以刘益的“正负开方术”为开端，经贾宪对二项式系数的深入研究发现了贾宪三角（他称为开方作法本源），建立了一般开高次方的方法，最终导致秦九韶对一般高次方程得到最一般的数值解法；以沈括（参见该条）的隙积术及隋唐时期的内插法为前提，朱世杰（参见该条）把垛积术与招差术（内插法）推进到一个崭新的水平；以历法中上元积年的计算及《孙子算经》“物不知数”问题的解法为先导，又受到《周易》占筮之法的启发，秦九韶创立了“大衍总数术”，给出了一次同余式问题的一般解，12世纪发展起来的天元术（设立未知数以建立方程的方法）在李冶手中已达到成熟，并由朱世杰发展成为处理可达四个未知数的一般高次方程组(建立、表示与消元)的方法——四元术.此外还有大量其他成果.为了处理数学研究中出现的大量新内容，又导致了新的数学方法的出现，数学书的理论化、系统化倾向也得到了增强.其中，秦九韶的《数书九章》(1247)年和朱世杰的《四元玉鉴》(1303年)是世界中世纪数学史上水平最高、内容最丰富的著作.
从元代后期开始，中国古代数学逐渐衰退了.在明代，数学的理论研究受到轻视，经典著作大多散失，数学中最重要的成果渐被遗忘.唯一的进步是计算技术的改进，主要是珠算的成熟与普及，及其应用范围的极大推广.这方面的代表作是明后期程大位的《算法统宗》(1592年).
1607年，徐光启与意大利传教士利玛窦合作翻译出版了欧几里得《原本》前6卷，定名为《几何原本》，从此，开始了西方数学传入与中西数学合流的时期，从而在独立意义上的中国古代数学的发展也就结束了.
纵观中国古代数学，其基本特点为理论的构造性与算法的程序性.从《九章算术》到宋元数学，其最重要的成果大都不外于此.可以说，这是一个以筹式演算为基本形式，以程序化算法为核心的机械化数学体系，强调实用，讲求效率，注重结果.其成果的最终形式，一般为简捷、统一的算法，漂亮的构造与漂亮的构图.在这方面我们可以举出大量的例证.包括中国古代数学的几个最重要的主题——高次方程数值解法，一次同余式组解法，垛积-招差术，天元术与四元术，比率理论，面积、体积理论，勾股定理等.在电子计算机已经深刻改变了数学面貌的今天，中国古代数学的一些基本思想与方法必将不断带给人们以新的启迪.

中国古代数学Zhongguo gudai shuxue

中国古代数学历史悠久，成就辉煌，具有与西方数学迥异的思想、方法和体系， 对世界数学的发展产生过重要影响。
新石器时代至东汉初期 (1世纪) 是中国数学萌芽、积累、逐渐形成体系的时期。在距今7000—5000年前的仰韶文化、河姆渡文化、大溪文化等的众多遗址中，发现了大量绘有各种几何图案的陶器，以及呈多种几何体的石器与陶器，其中有对圆周的十几乃至80等分，有多达15个的同心圆，在大溪文化中发现了许多带有镂孔的空心陶球， 有的陶球上画出三个两两垂直相交的大圆，交点处均有镂孔，在由三个镂孔及其联线形成的球面等边三角形的中心， 又有三条大圆弧与三个镂孔相连， 整个球面被划分为24个球面等腰三角形，体现了高超的几何认识能力。在距今约6000年前的西安半坡遗址及稍晚的上海马桥、山东城子崖遗址，刻划记数符号呈现出惊人的一致性， 并且明显属于十进制系统。殷商甲骨文(公元前13—前11世纪)中已有一至十及百、千、万的数名，有了三万这样的大数和简单的数字运算，出现了 “规”、“矩”二字，表明这两种基本作图工具早已产生。

甲骨文中的数字

西周时(公元前11世纪—前771)，数学成为贵族子弟必修的 “六艺”之一，称为 “九数”，可见内容较为丰富并已作了分类。成于周初的《易经》中已有初步的排列知识(八卦，六十四卦)。九数与八卦被历代学者认为是中国古代数学的重要源泉。
春秋时代(公元前770—前476)算筹已广泛使用。据后来的记载， 1—9的算筹表示有两种方式：
记多位数时，个位用纵式，其余各位纵横相间，遇空位则不摆放算筹。自然数与分数运算已经完备。不晚于战国(公元前475—前221)，出现了河图与洛书（如图），其中洛书是世界上最古老的三阶幻方。
春秋战国时期出现了理论几何学的雏形， 得到了

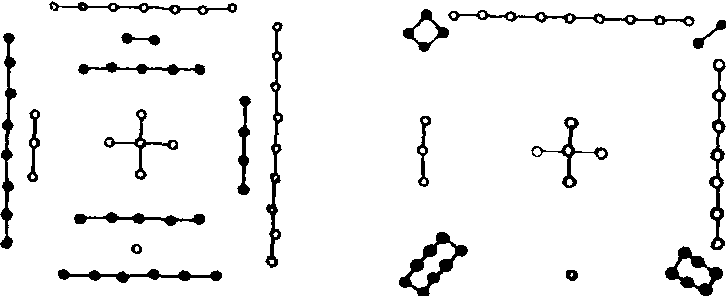
河图 洛书

许多含义深刻的命题，如《庄子·天下》：“矩不方，规不可以为圆”， “一尺之棰， 日取其半，万世不竭”；《墨经》： “圜，一中同长也”， “穷，或(即 “域”)有前不容尺也”。《考工记》中有了角度概念的萌芽，天文测量中广泛使用了平行线。
公元前2世纪初的 《算数书》（参见该条）标志着中国数学已初步形成体系。公元前100年左右的天文数学著作《周髀》(参见“算经十书”)记载了分数运算、等差数列、矩的用法及一般形式的勾股定理。然而真正具有划时代意义的， 是成书于公元前1世纪至公元1世纪的 《九章算术》（参见该条）。它系统地总结了 自先秦直到汉代的数学成果， 标志着中国初等数学理论体系的确立，其丰富的内容、方法与思想，成为后世数学发展的典范与源泉。
东汉初至五代末(10世纪)是中国数学持续发展与理论体系深化完善的时期。3世纪，赵爽注《周髀》，用弦图 （如图） 简捷而精彩地证明了勾股定理和许多勾股恒等式。263年刘徽的《九章算术注》对古代数学的概念、成果、方法及思想进行了全面的整理和发展(参见“刘徽”)，是中国数学史上具有高度理论创造性的杰作。

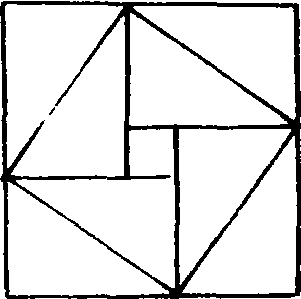
弦图

南北朝时，祖冲之（参见该条）在其名著《缀术》中得到精确到7位小数的圆周率，其子祖暅以刘徽的球体积研究为基础概括出“刘祖原理”，严格地证明了球体积公式(参见“祖冲之”)。《孙子算经》中的“物不知数”问题、《张丘建算经》中的“百鸡问题”开中国不定分析研究先河，并曾传入印度、阿拉伯及欧洲(参见“算经十书”、“物不知数”、“百鸡问题”)。
隋唐时期，由于天文学的推动，刘焯(544—610)、一行（参见该条）先后创立了等间距与不等间距二次内插法。受印度正弦表影响，一行创制了正切表。唐初，王孝通（参见该条）在其《缉古算经》中广泛研究了三次方程，体现了中国古代几何与代数紧密结合的特征。这一时期，数学教育已制度化，对机构、教师、学生、待遇、学制、考试、教科书等都有明确规定。同时，中国数学对朝鲜、日本产生了深远影响，并与印度数学进行了交流。许多成果由中国传入印度后，又经阿拉伯传入欧洲，对世界数学的发展起了很大作用。
宋代至元初(10—13世纪)是中国古代数学的高峰期，数学在内容、方法与形式上都发生了飞跃。11世纪，刘益创“正负开方术”，打破了方程系数仅取正数的限制，贾宪（参见该条）深入研究了二项式系数与高次开方法，最终由南宋秦九韶（参见该条）完成了一般的高次方程数值解法。以沈括（参见该条）的隙积术及隋唐时期的内插法为前提，朱世杰（参见该条）把垛积术与招差术（内插法）推进到一个崭新的水平。以历法中上元积年的推算及《孙子算经》“物不知数”问题的解法为先导，秦九韶创立“大衍总数术”，给出了一次同余式组的一般解法。12世纪发展起来的“天元术”(参见“李冶”)在李冶手中已达到成熟，朱世杰（参见该条）则将其发展成处理可达四个未知数的一般高次方程组(建立、表示与消元)的方法——四元术。此外，李冶对勾股容圆问题的研究，王恂(1235—1281)、郭守敬(1231—1316)对弧矢割圆术的研究、杨辉的纵横图（幻方）研究都达到了很高水平。为了处理数学研究中出现的大量新内容，又导致了新的数学方法的出现，数学书的理论化、系统化倾向也明显增强。其中，秦九韶的《数书九章》(1247)、和朱世杰的《四元玉鉴》(1303)是世界中世纪数学史上水平最高、内容最丰富的著作。
宋元时期，在理论数学成果大量出现的同时，计算技术也有了明显的进步。在数字记法上，由传统的算筹记数演变出一种书写形式的数码， 在秦九韶和李冶的著作中还使用了用以表示空位的中国式零号， 它最早出现于金代的《大明历》(1180)中。这套数码在明代演变成了广泛用于商业中的“暗码”（如图）。在秦、李二人的著作中还出现了明确的小数概念和表示法， 比欧洲人发明十进小数早了280年以上(以1530年鲁道夫的工作为准)。
然而，最引人注目的是珠算（参见该条）的发明和推广这是中国古代计算技术最重大的变革。
从元代后期开始，中国古代数学逐渐衰退了。在明代，数学的理论研究受到轻视，经典著作大多散失，数学中最重要的成果渐被遗忘。稍为可观的进步只有商业数学的发展和珠算的普及，其代表作是吴敬的《九章算法比类大全》 (1450) 和程大位的 《直指算法统宗》(1592)。1607年， 徐光启与意大利传教士利玛窦(Matteo Ricci,1552—1610)合作翻译出版了古希腊欧几里得《原本》的前6卷，定名为《几何原本》（参见该条）, 从此开始了西方数学传入与中西数学合流的时期， 独立意义上的中国古代数学的发展至此已经结束了。
从明末至清末， 较为重要的数学工作与历史事件有：明末至清初西方初等数学的传入，包括几何学、算术、三角学、对数、计算器械等。清初梅文鼎对初等数学会通中西的研究。在康熙皇帝支持下，初等数学全书《数理精蕴》的编纂(1713—1722)。受西方透视学影响，年希尧 (约1671—1738) 写成富有创见的透视学专著《视学》(1729)。明安图(约1692—约1763)深入研究传教士介绍的关于圆周率、正弦及正矢函数的三个无穷级数，积30多年心血，利用自创的割圆连比例法与级数反演方法给出证明， 并得到6个新的无穷级数。19世纪初，无穷级数研究更加广泛和深入，获得三角函数、反三角函数、对数函数的许多重要展开式，并导致了项名达、戴煦对有理指数的二项式定理的研究以及李善兰的尖锥术这一具有微积分思想的重要成果。清中期对传统数学的发掘与整理， 挽救了濒于失传的 《算经十书》和一批宋元数学名著，并引起了人们对传统数学的兴趣，其中较有创造性的是焦循的运算律研究，汪莱与李锐的方程论研究、汪莱的进位制研究，以及李善兰对垛积术的系统总结与全面发展。1857年，李善兰与英国传教士伟烈亚力合译的《几何原本》后九卷出版，1859年又译成传入中国的第一本符号代数著作《代数学》、第一本解析几何与微积分著作《代微积拾级》。从此，西方近代数学开始系统地传入中国， 为现代数学研究在中国的开端做了准备。
从《九章算术》到宋元数学，中国古代数学表现出极为明显的特征： 它是一个以位置制的筹式演算为基本形式，以程序化算法为核心的机械化、构造性数学体系，强调实用，讲求效率，注重结果。其成果的最终形式，一般为简捷、统一的算法，漂亮的构造与漂亮的构图。它的一些最重要的主题——比率理论，线性方程组理论，面积、体积理论，勾股理论，高次方程数值解法，一次同余式组解法，垛积—招差术，天元术与四元术，纵横图等，无一例外地表现出上述特征。在电子计算机已经深刻地改变了数学面貌的今天， 中国古代数学的一些基本思想与方法仍将带给人们新的启迪。