两个平面垂直的判定定理
两个平面垂直的判定定理liangge pingmian chuizhi depanding dingli
若一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.
如图1,若α⊥α,α⊂β,则α⊥β.
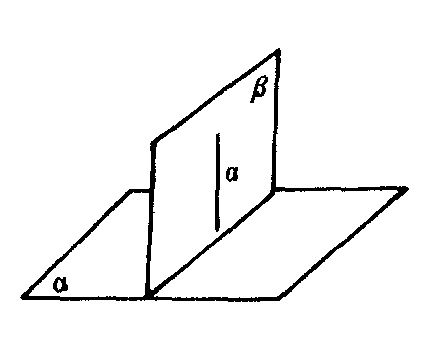
图1
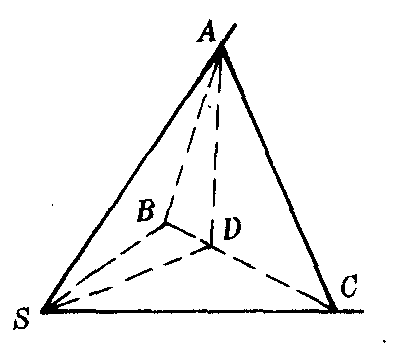
图2
上述定理是判定两个平面互相垂直的依据,而且也是找出垂直于一个平面的另一个平面的依据.
例 如图2,过S引三条不共面的直线,使∠ASB=∠ASC=60°,∠BSC=90°,并截取SA=SB=SC.求证平面ABC与平面BSC垂直.
证 因为SA=SB=SC,∠ASB=∠ASC=60°,所以△ASB和△ASC是两个全等的等边三角形.因此AS=AB=AC.作AD⊥平面BSC,D是垂足.由于过A点所引平面BSC的三条斜线段相等,所以它们的射影DB,DS,DC相等.因此D是△BSC的外心.因为∠BSC=90°,所以D是斜边BC的中点.因此,平面BSC的垂线AD在平面ABC内,所以平面ABC⊥平面BSC.
☚ 两个平面互相垂直 两个平面垂直的性质定理 ☛
- 奧府是什么意思
- 奧庰是什么意思
- 奧房是什么意思
- 奧秘是什么意思
- 奨是什么意思
- 奩是什么意思
- 奩具是什么意思
- 奩匣是什么意思
- 奩幣是什么意思
- 奩田是什么意思
- 奩箱是什么意思
- 奩資是什么意思
- 奩軸是什么意思
- 奪是什么意思
- 奪倫是什么意思
- 奪勞是什么意思
- 奪命丹是什么意思
- 奪氣是什么意思
- 奪爵是什么意思
- 奫是什么意思
- 奫沦是什么意思
- 奬是什么意思
- 奭是什么意思
- 奭多是什么意思
- 奭日是什么意思
- 奭然是什么意思
- 奭良是什么意思
- 奭酣是什么意思
- 奮是什么意思
- 奮布衣是什么意思
- 奮戟是什么意思
- 奮振是什么意思
- 奮榮是什么意思
- 奮發是什么意思
- 奮筆是什么意思
- 奮翅是什么意思
- 奮翼是什么意思
- 奮翼麟是什么意思
- 奮肆是什么意思
- 奮舋是什么意思
- 奮蕱是什么意思
- 奮藻是什么意思
- 奮迅是什么意思
- 奮隼是什么意思
- 奮鬣是什么意思
- 奮鱗是什么意思
- 奯是什么意思
- 奯目是什么意思
- 奰是什么意思
- 奰
.jpg) 是什么意思
是什么意思 - 奰
.jpg) 是什么意思
是什么意思 - 奰屃是什么意思
- 奱是什么意思
- 奲是什么意思
- 奲都是什么意思
- 女是什么意思
- 女䴷是什么意思
- 女丁是什么意思
- 女七岁是什么意思
- 女丈夫是什么意思