上确界
上确界shangquejie
非空实数集E的上确界指的是这样的实数a,对于E中任一个数x,都有x≤a,并且,对于任一正数ε,总有E中一个数x0,满足x0>a-ε.数集E的上确界通常记作supE.例如,闭区间〔0,4〕的上确界是4,数集{1,3/2,5/3,…,(2n-1)/n,…}的上确界是2.数集的上确界也是这个数集的上界中最小的数.
由有限个实数组成的数集必有上确界,它就是这个数集的最大数.没有上界的实数集不可能有上确界.
根据实数的理论,证明了一个定理:任意一个非空的有上界的实数集存在着唯一的上确界.这个定理在一定意义上刻画了实数的连续性特征.
☚ 下界 下确界 ☛
- 青鳞子是什么意思
- 青鳞魪是什么意思
- 青鳥是什么意思
- 青鳧是什么意思
- 青鴛是什么意思
- 青鴛刹是什么意思
- 青鵁是什么意思
- 青鵰是什么意思
- 青鵽是什么意思
- 青鷄是什么意思
- 青鸐是什么意思
- 青鸞是什么意思
- 青鸟是什么意思
- 青鸟不传云外信,丁香空结雨中愁.是什么意思
- 青鸟不传云外信,丁香空结雨中愁。是什么意思
- 青鸟不来天也老,断魂些,清霜静楚江。是什么意思
- 青鸟不来难问,玉妃几度仙游。是什么意思
- 青鸟书是什么意思
- 青鸟传信是什么意思
- 青鸟传音是什么意思
- 青鸟使是什么意思
- 青鸟来去闲,红霞朝夕变。是什么意思
- 青鸟栖居之所是什么意思
- 青鸟殷勤是什么意思
- 青鸟氏是什么意思
- 青鸟沈沈音尘绝,烟锁蓬莱宫殿。是什么意思
- 青鸟自爱玉山禾,仙禽徒贵华亭露。是什么意思
- 青鸟迎孤棹,白云随一身。是什么意思
- 青鸟集是什么意思
- 青鸡是什么意思
- 青鸡子是什么意思
- 青鸬是什么意思
- 青鸭是什么意思
- 青鸭化童是什么意思
- 青鸳是什么意思
- 青鸳刹是什么意思
- 青鸳剎是什么意思
- 青鸾是什么意思
- 青鸾信杳是什么意思
- 青鸾影孤是什么意思
- 青鸾思是什么意思
- 青鸾泣镜是什么意思
- 青鸾翼是什么意思
- 青鸾舞镜是什么意思
- 青鸾舞镜,红鸳交颈,是什么意思
- 青鹊是什么意思
- 青鹪是什么意思
- 青鹳[t
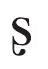 u
u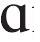
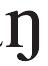 ]是什么意思
]是什么意思 - 青鹽是什么意思
- 青麈是什么意思
- 青麐麟是什么意思
- 青麓是什么意思
- 青麓书院是什么意思
- 青麓塔是什么意思
- 青麟丸是什么意思
- 青麦毛子是什么意思
- 青麻是什么意思
- 青麻是什么意思
- 青麻叶是什么意思
- 青麻叶大白菜是什么意思