万能三角代换
万能三角代换wanneng sanjiao daihuan
又称万能变换.即用半角的正切表示出解析式中所有的单角三角函数,以便解决问题这种方法.对于只含有单角三角函数sinx,cosx,tgx,…的三角式,通过万能三角代换,便化成只含tg(x/2)的三角式,若再设tg(x/2)=t,则化成不含三角函数的关于变量t的解析式.这在解三角方程,计算不定积分或其他问题中常是有效的.
例如,解三角方程sinx-2cosx=2.设tg(x/2)=t,原方程化为代数方程
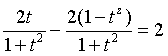
☚ 三角代换 万能代换公式 ☛
- 俄林,b.是什么意思
- 俄林,b·g·是什么意思
- 俄林,伯蒂尔是什么意思
- 俄林,贝蒂尔·戈特哈德是什么意思
- 俄柯河是什么意思
- 俄格绰特巴是什么意思
- 俄梅戛是什么意思
- 俄梅珥是什么意思
- 俄汉、汉俄对照语言学名词是什么意思
- 俄汉、汉俄常用词词典是什么意思
- 俄汉、英汉苏军译名手册是什么意思
- 俄汉世界地名翻译手册是什么意思
- 俄汉世界地名译名手册是什么意思
- 俄汉仪器仪表与自动化技术词典是什么意思
- 俄汉体育词汇是什么意思
- 俄汉兵工辞典是什么意思
- 俄汉兽医学词典是什么意思
- 俄汉军事医学词汇是什么意思
- 俄汉军事缩略语大词典是什么意思
- 俄汉农业机械化电气化辞典是什么意思
- 俄汉农业词典是什么意思
- 俄汉冶金工业词典是什么意思
- 俄汉动物学词汇是什么意思
- 俄汉动物生态学名词是什么意思
- 俄汉勘探地球物理地球化学词典是什么意思
- 俄汉化学化工与综合科技词典是什么意思
- 俄汉化学化工缩略语词典是什么意思
- 俄汉化学化工词汇是什么意思
- 俄汉医学词汇是什么意思
- 俄汉历史辞典是什么意思
- 俄汉双解俄语方言词典是什么意思
- 俄汉双解俚语词典是什么意思
- 俄汉双解实用交际词典是什么意思
- 俄汉双解小词典是什么意思
- 俄汉双解文学形象小词典是什么意思
- 俄汉双解文学形象词典是什么意思
- 俄汉双解详解辞典是什么意思
- 俄汉国际经贸会话手册是什么意思
- 俄汉图解词典是什么意思
- 俄汉土木建筑工程辞典是什么意思
- 俄汉土质学及土力学词汇是什么意思
- 俄汉地球物理词典是什么意思
- 俄汉地质学缩写词汇是什么意思
- 俄汉外贸用语词典是什么意思
- 俄汉大气科学缩略语词汇是什么意思
- 俄汉大辞典是什么意思
- 俄汉字典是什么意思
- 俄汉学生词典是什么意思
- 俄汉对照冶金专业常用词汇编是什么意思
- 俄汉对照冶金常用词汇编是什么意思
- 俄汉对照化学专业常用词汇编是什么意思
- 俄汉对照医学专业常用词汇编是什么意思
- 俄汉对照地理专业常用词汇编是什么意思
- 俄汉对照地质、地化专业常用词汇编是什么意思
- 俄汉对照地质专业常用词汇编是什么意思
- 俄汉对照心理学专业常用词汇编是什么意思
- 俄汉对照数学专业常用词汇编是什么意思
- 俄汉对照文艺学专业常用词汇编是什么意思
- 俄汉对照机械专业常用词汇编是什么意思
- 俄汉对照物理专业常用词汇是什么意思