一元四次方程
一元四次方程yiyuan sici fangcheng
在数域F上只含有一个未知数的四次方程.关于x的一元四次方程的一般形式是
a4x4+a3x3+a2x2+a1x+a0=0 (a4≠0) (1)
在复数集内,一元四次方程有且仅有四个根.在中学数学课中所研究的一元四次方程都是一些特殊的形式,可以用一些特殊的方法求解.一般的一元四次方程的代数解法,曾经是代数学的一个中心问题,到16世纪才得到解决.一元四次方程的代数解法有多种,其中的一种是:设 y=x+a3/4a4,并代入方程(1),可得到一个缺项四次方程
y4+py2+qy+r=0 (2)
令
y4+py2+qy+r=(y2+ky+l)(y2-ky+m)
比较两端系数,得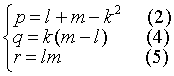
若 q≠0,则k≠0.则由(3),(4)解得
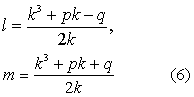
k6+2pk4+(p2-4r)k2-q2=0 (7)
又令k2=u,则方程(7)化为u的三次方程u3+2pu2+(p2-4r)u-q2=0 (8)
用一元三次方程求根公式(参阅“卡丹公式”)可求得方程(8)的一个根u0,从而可求出(7)的一个解k0,并将其代入(6)解得l=l0,m=m0,于是方程(2)化为(y2+k0y+l0)(y2-k0y+m0)=0
因此,由解方程y2+k0y+l0=0和y2-k0y+m0=0
可求得方程(2)的四个根分别为y1,y2,y3,y4.则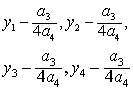
☚ 一元三次方程的求根公式 一元n次方程 ☛
- 诺劳孜是什么意思
- 诺劳孜节是什么意思
- 诺南综合征是什么意思
- 诺卡氏菌属是什么意思
- 诺卡菌是什么意思
- 诺只么是什么意思
- 诺合是什么意思
- 诺哲是什么意思
- 诺唯是什么意思
- 诺因·乌拉是什么意思
- 诺坎尔是什么意思
- 诺埃尔·希利亚德 毛利姑娘是什么意思
- 诺基亚不要赢,只要不out是什么意思
- 诺基亚公司是什么意思
- 诺基亚(芬)是什么意思
- 诺夫哥罗得审判法规是什么意思
- 诺夫哥罗德是什么意思
- 诺夫哥罗德之战是什么意思
- 诺夫哥罗德公国是什么意思
- 诺奎,j.是什么意思
- 诺奖是什么意思
- 诺如孜节是什么意思
- 诺如金是什么意思
- 诺姆是什么意思
- 诺宜斯求偿案是什么意思
- 诺实和玉丹是什么意思
- 诺尔是什么意思
- 诺尔卫是什么意思
- 诺尔图浩图布沟是什么意思
- 诺尔布是什么意思
- 诺尔布事件是什么意思
- 诺尔布扎布是什么意思
- 诺尔布扎那是什么意思
- 诺尔布敦多克是什么意思
- 诺尔布林沁是什么意思
- 诺尔布班第是什么意思
- 诺尔德是什么意思
- 诺尔扎是什么意思
- 诺尔斯,s. h.是什么意思
- 诺尔曼·白求恩断片是什么意思
- 诺尔本是什么意思
- 诺尔特沟是什么意思
- 诺尔特湖是什么意思
- 诺尔特达坂是什么意思
- 诺尔特阿苏山口是什么意思
- 诺尔艾肯沟是什么意思
- 诺尔贝希是什么意思
- 诺尔迪是什么意思
- 诺尔雷平是什么意思
- 诺岷是什么意思
- 诺州是什么意思
- 诺布尔是什么意思
- 诺布尔位置是什么意思
- 诺布尔手术是什么意思
- 诺布尔,c.s.是什么意思
- 诺布尔,约翰·威洛克是什么意思
- 诺布雷是什么意思
- 诺延是什么意思
- 诺延出钟根是什么意思
- 诺延达喇是什么意思