x→x时函数的极限

x→x₀时函数的极限x→x₀ shi hanshu de jixian

设函数f (x)在点x₀的某一空心邻域内有定义，若x以任何方式无限接近x₀时，对应的函数值f (x)无限接近常数a，则a叫做函数f (x)当x趋于x₀时的极限。更精确地说，就是：
设函数f (x)在点x₀的某个空心邻域内有定义，a是一个常数.若对任给的正数ε，都存在某一个正数δ，使得当0<|x-x₀|<δ时，总有|f (x)-a|<ε，则称当x趋于x₀时f (x) 的极限为a，记作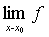(x) =a, 或f (x)→a (x→x0) x。x₀
在上述定义中，正数ε表示f(x)与a的接近程度，δ表示使f(x)与a接近到ε时x与x₀的接近程度，ε可以任意给定，而δ与ε有关 (也与x0有关)。“当0=|x-x₀|<ε时，总有|f (x)-a| <ε”表示，只要x充分接近x₀,f (x)就可以充分接近a. “0< |x-x₀|”指出，当x→x₀时，始终有x≠x₀。这说明，当x→x₀时，f(x)的极限与f (x)在x₀是否有定义无关，而只与f(x)在点x₀附近的函数值的变化有关。

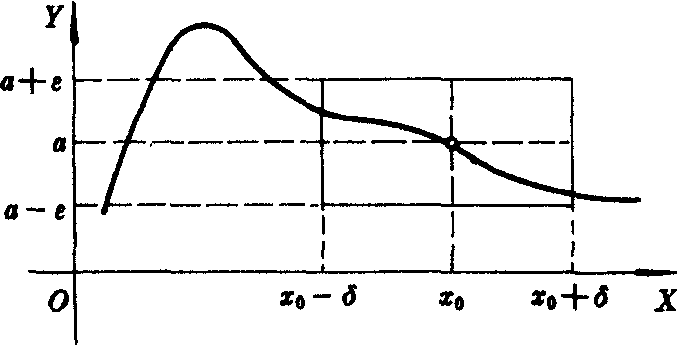
极限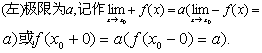的几何意义是，对于以直线y=a为中心线，宽为2ε的无论怎样窄的横带，必存在以直线x=x0为中心线，宽为2δ的直带，使曲线y=f (x)在直带内的部分全部落在横带内，但点(x₀,f (x₀))可能例外或无意义 （如上图）。
函数极限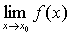的定义，是连续性、导数等重要定义的依据. 极限方法用于研究微积分中的理论问题(如连续函数的性质，可积性理论等)，也是一种重要的基本方法。因此，函数极限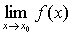是微积分的最基本的概念之一。