F检验F jianyan

利用服从F分布的统计量进行假设检验的方法。F分布是统计检验中常用的一种随机变量的概率分布，F分布有两个参数：分子自由度和分母自由度。利用F分布进行假设检验的基本步骤是：首先找出与所检验假设有关的服从F分布的统计量，计算该统计量的值，然后从F值表中查出相应的临界值，将计算得出的统计量的值与临界值进行比较，由此得出结论。F检验的主要用途有：
❶两个独立样本的总体方差齐性检验；
❷在单因素（即自变量）实验设计中检验因素各水平的效应是否有差异；
❸在多因素实验设计中检验每一因素各水平的效应是否有差异，以及检验各因素之间是否存在交互作用；
❹检验复相关系数是否为0。[例]随机抽取男生31名，女生25名，进行闪光融合频率的测定，结果男生的方差为36，女生方差为81，试问男女生闪光融合频率的方差是否有显著差异？解：n1=31,n2=25 S21=36,S22=81

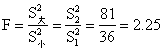
分子自由度df=n2-1=25-1=24
分母自由度df=n1-1=31-1=30查F值表得：

F.05/2(24, 30) =2.14
故F＞F.05/2(24, 30),＜.05

因此，男女生闪光融合频率的方差在.05水平差异显著。

F检验F-Test

显著性检验的方法之一。根据两个容量分别为N₁的N₂的独立随机样本的方差S₁²和S₂²推断两个正态总体的方差σ₁²和σ₂²是否相等的检验。检验的零假设H₀:σ₁²＝σ₂²备择假设H_A:σ₁²≠σ₂²。给定显著性水平α(0<α<1)，计算出S₁²和S₂²。两个总体方差的无偏估量分别是N₁S₁²/(N₁-1)和N₂S₂²/(N₁-1)，它们分别除以各自的总体方差σ₁²和σ₂²。后两者的比率：

遵循第一自由度为N₁-1第二自由度为N₂-1的F分布。故显著性检验应按F分布进行。因

若H₀为真，则F₀的值应近于1；否则表明H₀可能不正确。

F检验

又称方差分析，数理统计中假设检验的方式之一。方差分析是对引起方差变化的各种因素进行分析比较，从而检验出形成各样本（各部分）差异的主要原因（因素），并与规定的理论F值相比较，以判定它们之间的差异是否显著。在舆论调查中，方差分析常根据样本统计值(E2或γ)来检验总体中的定类与定距、定序与定距、定距与定距变量之间是否相关。其检验步骤为：（一）根据已有资料建立假设，确定显著性水平a，查F值表得到否定域的临界值；（二）由样本资料计算F值；（三）将计算所得F1值与临界值（负值取绝对值）进行比较，若计算值大于临界值，则否定H0，反之，则承认H0。如果样本统计值为相关比率E2，则F值的计算公式为：。式中，df1为分子的自由度，df1=k-1,df2为分母的自由度，df2=n-k，其中k为x变量的类别数，即分组的数目，n为样本个案数。若样本统计值为相关系数γ，除了将上式中的E2换成γ之外，其余的符号和关系均不变。在舆论研究中，方差分析的另一个用途是进行方差的一致性检验。这时的研究假设为总体内两部分方差不相等，虚无假设为总体内两部分方差相等。F的计算公式为：F=S12/S22。式中，S12为样本中较大的一组方差，S22为样本中较小的一组方差。在计算F值时，S12与S22都是根据原始数据求出离差平分和再除以自由度n-1得到的。若计算所得的F值大于规定的某一显著性水平下的临界值，则否定虚无假设，说明总体中两部分方差不相等，即无一致性或差异显著；反之则接受虚无假设，即承认总体中两部分方差相等或具有一致性。可以把方差分析看成是两个样本均值差分析的推广。因为在检验的假定上，方差分析与均值差分析基本相同。但是就其检验本身来说却又有不同。两个样本的均值差的分析是假定正态分布和独立随机的样本等总体标准差和总体平均值相等的零假设(H0)。方差分析检验的方法本身直接涉及方差而不是均值和标准差。方差分析的意义就在于：当用t分布检验两个总体的均值差时，是假定二者都具有相同的方差(a2)。为检验这种假设是否合理，必须有一种可以检验方差同一性的分布即F分布，用F分布即可检验方差的同一性。方差分析的检验方法是比较两个总体方差的估计量，并不取两种估计量之差，而是取第二种估计量对第一种估计量的比率，至于这个比率大到什么程度才可以对零假设提出怀疑，则通过两种估计量的比率F值来确定。求F值需查F表，该表是根据F分布编制的，较为复杂。

F检验F-test

运用服从F分布的统计量或方差比所做的统计检验。F检验有广泛的用途：❶检验两个独立样本的总体方差的齐性；
❷在一个分类基础上或在一个维度上检验各处理效应是否有差异；
❸分析多个维度设计中，每一维度的各个处理效应是否有差异，以及是否存在各个维度之间的交互作用；
❹检验总体的复相关系数是否为0;
❺检验总体的相关比是否等于0;
❻检验回归是否为直线回归等等。进行F检验需要满足的条件是：❶总体的正态性；
❷抽样的随机性和独立性；
❸方差分析中的效应的可加性；
❹方差分析中的组内方差的齐性。若这些条件不能满足，F检验的有效性就会受到影响，F检验常用于方差的齐性检验。在只有两个样本方差时，F=S²₁/S²₂，分子是较大的那个方差。求出F值后，按df₁＝n_1-1,df₂＝n_2-1查F分布表，若F> F_0.05，则两个方差不齐。计算df时使用的n₁是S²₁所来自的样本容量，n₂是S²₂所来自的样本容量。方差分析后的F检验也与上述方法类似。

F检验F test

运用服从F分布的统计量或方差比所作的统计检验，又称“变异数分析”或“方差分析”，参数检验的一种。它以分析平方和为基础，可同时检验两个以上数据组之间的差异显著性。其计算公式如下：
总和方(SST)=组内和方(SSW)+组间和方(SSB)

上式中X为原始数据， 为组内平均数， 为总平均数，dfB为组间自由度，dfW为组内自由度，k为组数，n为组内的数据个数，VB为组间变异数，VW为组内变异数。F比率是组间变异数(VB)与组内变异数(VW)的比值。如各组平均数都来源于同一总体，组间变异数与组内变异数在理论上应该相等，F值接近或等于1。如果F比值大于1，则各组数据属于同一总体的可能性就很少。在作F检验时，如实得的F值大于F₀.₀₅，就要否定零假设(1=2=…=k)认为各组的平均数的差异是显著的，如实得的F值大于F_0.01，就认为各组的平均数的差异是非常显著的。反之，则接受原假设。应注意的是，F检验中的F比值是一个综合指标，它只笼统地表明各实验组间是否存在着差异，但到底哪些变量对实验结果发生影响，影响程度有多大， 尚需进一步用最小显著差异检验法对各组平均数进行多重比较检验。以确定各对平均数何者显著，何者不显著。当研究涉及到两个或多个变量在不同条件下的差异时，这就不但要检验每个变量在不同条件下的差异，而且还要考察各变量之间的交互影响，这时就需要采用多因素方差分析法。

F检验F-test

检验统计量是否服从或渐进服从F分布的参数检验方法。主要用于实验设计中数据的处理，分析数据方差的不同来源。在检验过程中需要满足的条件是： (1) 数据总体分布呈正态或渐进正态；(2) 抽样的随机性和独立性；(3) 方差分析中的效应可加性；(4) 方差分析中组内方差齐性。

F检验

参数检验的一种。检验统计量服从或渐近服从F分布的检验。在检验过程中需要满足以下条件： (1) 总体分布呈正态或渐近正态；(2) 抽样的随机性和独立性；(3) 方差分析中的效应可加性；(4) 方差分析中组内方差齐性。