3n+1问题3n+1 wenti

任取一个正整数n，若n是奇数，就乘以3再加1；若n是偶数，就除以2。我们把这两种步骤表示为下列函数：
对所得结果重复上述步骤， 不断得到新的数。
假如我们最初选取的数是3, 于是：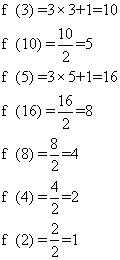
当得出1时就没有必要再算下去了。因为
f (1) =3×1+1=4
于是将出现1→4→2→1的无限循环。因此，如果初值是3，经过7次运算，我们得到了一列有顺序的数（称为一个序列）:
3, 10, 5, 16, 8, 4, 2, 1
现在我们取初值为7，经过类似的运算，将得到另一个序列：
7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10,
5, 16, 8, 4, 2, 1
我们发现： 似乎不论n的初值如何选取， 所得到的序列最后总是以1结束。这个结论正确吗？
其实，这正是数论中一个十分著名的猜想。对于一个选定的正整数n，求出相应的序列并不难，困难之处在于：能否对所有的正整数n求出一个一般的解答。到目前为止，人们已经对许多正整数做过明显的试验，结果都符合上面的猜想。例如，日本东京大学的米田信夫对2⁴⁰(大约相当于1. 2万亿)以下的所有正整数都进行过试验，经过有限次运算后，每个序列都以1结束。尽管如此， 至今却没有人能够对全体正整数证明这一猜想。不论你对多少个正整数做过试验，仍然只是有限个，而正整数的全体却是无穷无尽的。几乎所有的数学家都相信这个猜想是正确的，却对它束手无策。很难说这个问题是数论中没有解决的问题中最重要的一个，但它肯定是最令人头疼的问题之一。
这个问题最初是由什么人提出的，已经不清楚了，但似乎并不古老。本世纪30年代，德国汉堡大学的学生考拉茨 (L. Collatz)就研究过它。自从50年代以来， 它在西方国家的许多大学的数学系和计算机系一再引起广泛的兴趣。在日本，这个问题被称为角谷猜想， 因为它是由角谷静夫介绍到日本的。角谷静夫1960年初次听到这个问题，他说：“有一个月耶鲁大学每个人都在研究这个问题，但没有任何结果。我到芝加哥大学提到这个问题之后，也出现同样的现象。有人开这样一个玩笑说， 这个问题是企图减缓美国数学研究的进展的阴谋的一个组成部分。”
3n+1问题及其各种推广形式至今仍以其巨大的魅力吸引着众多的研究者。