频率稳定度

---

任何频标内都存在噪声，主要有快速变化的白噪声，较慢变化的闪变噪声和更慢变化的无规行走噪声。这些噪声会对频标输出信号的相位和频率进行调制，结果引起频率随机性的变化。定量的描述这种变化程度的量称为频率稳定度。

如前所述，实际测量时只能得到频率在一段时间内的平均值，即y(τ)值。在描述频率稳定度时，平均时间τ称为取样时间，取样时间不同，y(τ)的起伏程度也不同，如图8．4－2所示。

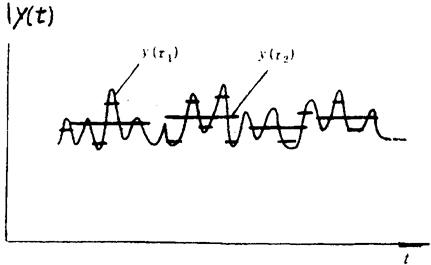
图8．4－2 频率的随机起伏

确切的说，频率稳定度是描述平均频率随机起伏程度的量，数学表征用Allan(阿兰)方差的平方根值。

为什么采用Allan方差，而不用一般统计学上的经典方差?详细论证要涉及到比较复杂的数学，这里只作些简单的介绍。

1．经典方差

设X为一随机变量，其无限个可能值的平均值称为数学期望，用E(x)表示

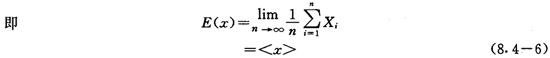
为推导方便，用符号〈…〉表示数学期望。

经典方差为

σ²=＜［x－＜x＞］²＞ (8．4－7)

表示随机变量x相对其数学期望的离散(起伏)程度。

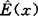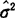实际测量时只能得到有限个值，通过计算求出无限平均的近似值，在统计学上称为估计值。分别用和表示。一个好的估计值应满足无偏性和一致性两点要求。由此有：

即随机变量有限个值的算术平均值就是其无限平均的最好估计值。

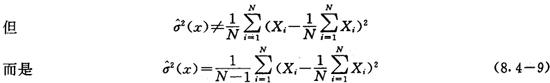
尽管当N足够大时，右式中除以N和除以N－1无多大差别，但理论上只有后者才满足无偏性的要求。

用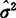作为σ²的估计值要有一个前提，即理论上证明σ²确实存在，实际测量计算时，随着N的加大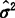，值应逐渐稳定，即是收敛的。在其他领域出现的随机变量几乎都满足这一前提，故(8．4－9)式一直被普遍使用。

1966年前美国国家标准局(NBS)的Allan博士在测试计算原子频标的稳定度时，发现随着N值的加大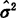，也跟着加大，并不趋向一个稳定的值，而呈发散状态。随后，他就进行理论推导，发现闪变噪声对频标信号的频率调制后，造成用(8．4－7)计算的经典方差是发散的，即不存在，或者说呈无限大值。这样，就无法用一个有限值去作为它的估计值。因而就不能再用频率这种随机变量的经典方差去描述它的起伏程度。Allan提出了一种改进的方差来表征频率稳定度，即Allan方差。

2．Allan方差

由于噪声调制的结果，使得相对平均频率编差y(τ)成为一个随机变量。其中闪变噪声的调频又造成y(τ)的经典方差呈发散特性。Allan对经典方差的估计值(8．4－9式)进行深入研究，发现此估计值的数学期望对各种噪声却都是收敛的。于是就提出可用这个数学期望表征频率的随机起伏，用σ_y²(τ)表式，即

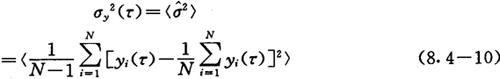
式中的N称为取样个数，即所测得的y(τ)的个数。此式的含意是每取N个y(τ)后即可算出一个估计值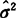，进行无数回测量，(注意每回测量时取样个数都是一样的)可得元数个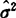值，取其平均即为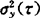。显然，N不同，所得的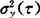值也不同。为统一起见，Allan建议取N=2，代入后可得。

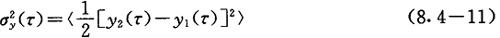
后来人们就把这个量称为Allan方差。由于每回测量只取两个y(τ)的值，进行无数回测量后再平均，所以又称为对方差。

同样，实际应用时，只能计算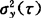的估计值，如前所述，一个随机变量(此处为［y₂(τ)－y₁(τ)］²)的无数次取样的平均值的无偏估计就是其有限取样的算术平均值。即

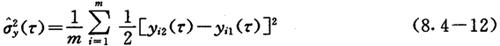
式中的m称为取样组数，每一组中只包含两个y(τ)值。此外，相继两次测量y(τ)时的间隔称为取样周期，用T表示T＞τ时称为间隙取样，T－τ为间隙时间；T=τ时为无间隙取样，理论上已证明，T／τ为不同值时，所得的Allan方差或其估计值也不同。所以Allan又建议，对于每一组内的两个y(τ)值采用无间隙取样。组与组之间有无间隙以及间隙的大小在理论上无影响。如图8．4－3所示。

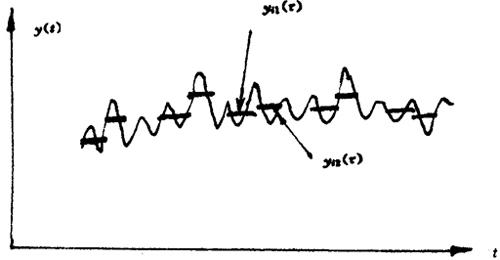
图8．4－3 Allan方差取样示意图

这样，y(τ)的实际取样个数将为2m。在实用时为节省总的测量时间，理论证明，如所有取样之间均无间隙，且y₁(τ)与y₂(τ)为一组，y₂(τ)与y₃(τ)为一组……。所计算的结果与按图8．4－3的取样方式计算结果是一样的，这样，总的取样个数可缩减到m+1个。计算公式可变为

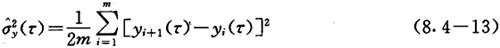
这就是目前Allan方差的实用定义式，而频率稳定度用它的平方根表征。并把符号简化为σy(τ)即：

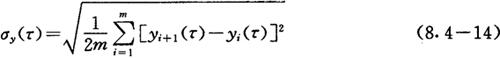
由于定义时要求取样是无间隙的，这会使测量设备变得复杂。通过理论证明和实验验证，可用有间隙取样代替，只要间隙时间小于5秒，代替后的误差会小于10%，这对频率稳定度的量值而言，可以忽略。故在实际测量时，可用无间隙取样，也可用有间隙取样，计算公式无变化。

最后是取样组数m的规定，一般当取样时间τ≤10s时，取m=100，τ≥100s时取m=30。这要看实际情况，特别当τ较大时，m太大令总的测量时间太长。故在我国检定原子频标的日稳定度(注意不要与日飘移率混淆)时，通常取m=15。

此外，还应指出(8．4－14)式给出的结果是Allan的方差的估计值的平方根值，故所计算的值σy(τ)也还是个随机变量。它意味着，对于同一频标的同一取样时间的稳定度，进行多次测定时，所得的结果是不一样的，但其差别不会超过。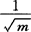

【参考文献】：

［1］王义遒等，量子频标原理，科学出版社，1986。

［2］吴守贤等，时间与频率，科学出版社，1983。

［3］黄秉英等，时间频率的精确测量，计量出版社，1986。

［4］王江现代测量技术，计量出版社，1987。

［5］P. Kartaschoff ,Frequency and Time,Academic Press ,1978.

［6］J. A. Barnes et al. ,Characterization of frequency stability, IEEE Trans Instrum Meas. IM —20,p.105—120,1971.

［7］Time and frequency:Theory and Fundamentals,NBS Manograph 140,1974.

［8］D. W. Allan ,The measurement of fruquency and frequency stability of precision oscillator,Proc.6th Ann PTTI Planning Meeting.

［9］Annual Report of the BIPM Time Sectina,1974.