随机事件和样本空间

---

随机现象 在一定条件下可能发生，也可能不发生的现象叫做随机现象．随机现象有两个特点：(1)在一次观察中，现象可能发生也可能不发生，即结果呈现不确定性；(2)在大量重复观察中，其结果具有统计规律性．

随机试验 具有以下几个特点的试验叫做随机试验，用E表示．

(1)试验具有明确的目的；

(2)在相同条件下，试验可以重复进行；

(3)试验的结果不止一个，所有结果事先都能明确地指出来；

(4)每次试验之前，不能确定会出现哪个结果．

随机事件 随机试验中每一个可能出现的结果叫做随机事件，用A，B，C表示．

(1)基本事件：试验中最简单的，不能再分的事件叫做基本事件．

(2)复合事件：由至少两个基本事件构成的事件叫做复合事件．

(3)必然事件：必定要发生的事件叫做必然事件．

(4)不可能事件：必定不会发生的事件叫做不可能事件．

样本空间 每一个基本事件叫做一个样本点；全体样本点的集合叫做样本空间，记作Ω．

样本空间是样本点的全集，样本点是样本空间的元素．样本空间是必然事件．

样本空间有以下三种类型：

(1)有限集合：样本空间中的样本点个数是有限的．

(2)无限可列集合：样本空间中的样本点个数是无限的，但可以列出来．

(3)无限不可列集合：样本空间中的样本点个数是无限的，又不能列出．

事件的关系

(1)包含关系：若事件B发生必然导致事件A发生，则称事件A包含事件B，记为．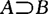

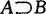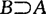(2)相等关系：若，且，则称事件A与事件B相等，记为A=B．

(3)事件的并：A∪B．若事件A，B中至少一个发生，则称事件A∪B发生．

(4)事件的交：A∩B=AB．若事件A，B同时发生，则称事件AB发生．AB又叫做事件A，B的积．

(5)互斥事件：若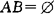，则称A与B为互斥事件(互不相容事件)．

(6)对立事件：若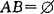且A∪B=Ω，则称A与B为对立事件，记为或，简称为A非，简称为B非．

(7)事件的差：A－B=A－AB=AB．

以上这些关系，可以用图形(也称文氏图)表示(见图1．1)．

图1．1 事件的关系

事件的运算规则

(1)交换律：A∪B=B∪A；A∩B=B∩A．

(2)结合律：A∪(B∪C)=(A∪B)∪C；

A∩(B∩C)=(A∩B)∩C．

(3)分配律：A∪(B∩C)=(A∪B)∩(A∪C)；

A∩(B∪C)=(A∩B)∪(A∩C)．

(4)德·摩根(De Morgan)律：；．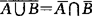

推广：对n个事件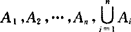i叫做n个事件的并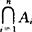；叫做n个事件的交(或积)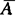，_i为A_i的对立事件，则有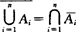称为“并的非等于非的交(积)”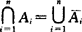；称为“交(积)的非等于非的并”．