线性子空间的定义

---

定义 S是数域F上的线性空间，W是S的非空子集，若W对S的两种运算(加法和数量乘法)仍构成一个线性空间，则W称为S的线性子空间．

W是S的子空间的充分必要条件 W是S的子空间的充分必要条件是线性空间S的非空子集W对于S的两种运算封闭，即W是S的子空间的充分必要条件是：

(1)W是非空集．

(2)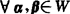，则α+β∈W．

(3)，则kα∈W．

W是S的子空间的必要条件

(1)S的零向量0在W中．

(2)若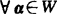，则－α∈W．

(3)，则

k₁α1+k₂α₂+…+k_rα_r∈W．

平凡子空间 线性空间S本身是S的一个子空间．

由S的单个零向量组成的集合也是S的子空间，称为零子空间．

以上两个子空间称为平凡子空间，其余子空间称为非平凡子空间．

生成子空间 设α₁，α₂，…，α_r是线性空间S的一组向量，它们的全部线性组合所成的集合非空，满足封闭性条件，故是S的子空间，称为由向量α₁，α₂，…，α_r生成的子空间，记作

L(α₁，α₂，…，α_r)．

等价向量组生成相同的子空间 两个向量组生成相同的子空间的充分必要条件是两个向量组等价．

生成子空间的维数 生成子空间L(α₁，α₂，…；α_r)的维数，等于向量组α₁，α₂，…，α_r的秩r(α₁，α₂，…，α_r)．

子空间的交 设W₁，W₂都是数域F上的线性空间S的子空间，则W₁，W₂的公共元素的集合记作W₁∩W₂，即

W₁∩W₂=｛αlα∈W₁且α∈W₂｝，

则W₁∩W₂也是S的子空间，称为子空间W₁，W₂的交．

子空间的和 设W₁，W₂都是数域F上的线性空间S的子空间，则集合｛α=α₁+α₂|α₁∈W₁，α₂∈W₂｝也是S的子空间，记成

W₁+W₂=｛α=α₁+α₂|α₁∈W₁，α₂∈W₂｝，

称为子空间W₁与W₂的和．

维数公式 设W₁，W₂是线性空间S的子空间，则公式

dimW₁+dimW₂=dim(W₁+W₂)+dim(W1∩W₂)

称为维数公式，且有以下关系：

(1)因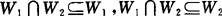，故

dim(W₁∩W₂)≤dimW₁，dim(W₁∩W₂)≤dimW₂．

(2)因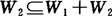，，故

dimW₁≤dim(W₁+W₂)，dimW₂≤dim(W₁+W₂)．

(3)若dimW₁+dimW₂＞dimS，则dim(W₁∩W₂)＞0．

(4)W₁∩W₂是S中既包含在W₁内，又包含在W₂内的最大的子空间．

(5)W₁+W₂是S中的既包含W₁又包含W₂的最小的子空间．

子空间的直和 设W₁，W₂是线性空间S的两个子空间，如果W₁+W₂中的每个向量α可表示成

α=α₁+α₂(其中α₁∈W₁，α₂∈W₂)，

且其表示法是惟一的，则称W₁+W₂为直和，记作．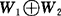

直和的充要条件 W₁，W₂是线性空间S的两个子空间，则

(1)W₁+W₂是直和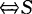中的零向量可表示成

0=α₁+α₂(其中α₁∈W₁，α₂∈W₂)，

其表示法是惟一的．

(2)W₁+W₂是直和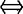

W₁∩W₂=｛0｝．

(3)W₁+W₂是直和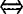

dim(W₁+W₂)=dimW₁+dimW₂．