线性回归分析

---

第一节介绍了依赖于一个数量因子x的总体族{Y_x，x∈T}的平均数EYx的线性模拟：

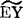x=β₀+βx (48．4。1)_i

x-y平面上的直线(48．4．1)₁式称为总体族的一元回归直线。必须注意到(48。4．1)₁式与(48．3．1)₁式在概念上的差别，它们分别称为“因子回归”与“相关回归”。

一元(因子)回归的调查和实验方案是{N；x_k，k=1—N；n}，表示数量因子x取N个值，这N个值是x_k，k=1—N(不妨设为从小到大的次序排列)，对应于每一个xk的总体Y_k的样本观测值是n个同质数据y_ki，i=1—n。本章只研究n=1的情形⁽¹⁾，借用二元总体的样本观测值的格式：=()。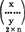

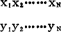β₀、β和一元回归直线(48．4．1)₁式的最小二乘估计跟(48。3．1)₂式在形式上一样：

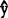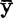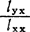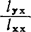_x=b₀+bx，其中：b₀=-X，b=(48．4．1)₂

直线(48。4．1)2式通过点(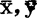)，并且一般地只适用于实验方案中数量因子的取值范围x∈〔x₁，x_N〕。

定义下列剩余平方和与回归平方和：

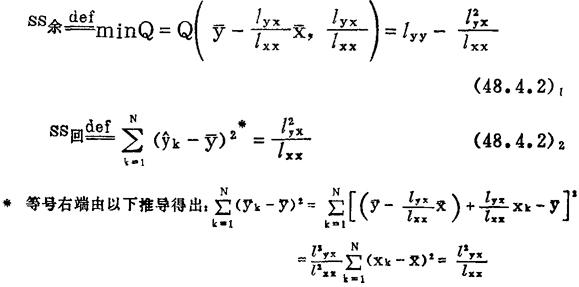
由以上二式可知：

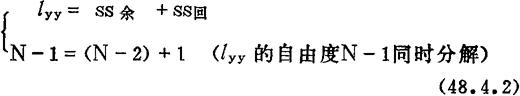
产生差异平方和l_yy的原因，除了随机因素而外，主要是由于N个总体Y_k(n=1的样本)的观测值y_k，k=1—N分别在因子x的N个取值x_k，k=1—N条件下产生。l_yy是N个非同质数据y_k，k=1—N与其平均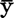的差异平方和，它在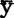被N个yk的最小二乘拟合值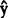_k分别取代以后减小⁽²⁾到SS余。由于分别k=1—N，观测值y_k与其最小二乘拟合值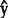_k=b₀+bx_k都是由x_k产生的，从而在构成SS余的差异y_k—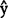_k中抵销了混杂在y_k—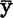中的因子x的N个取值的影响(注意，还保留有只在n>1情形才能进行分析的模式误差，即失拟)。l_yy减小到SS余的减小部分SS回表示一元回归直线(48．4．1)₂式对于差异平方和的减小所作出的“贡献”。由此，对于每一x∈〔x₁，x_N〕，分别用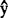x作

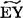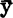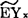为_x的估计值，优于对所有x∈〔x₁，x_N〕一律用常数作为的估计值。

需要定义下列方差以及F：

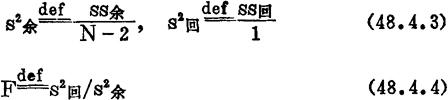
如果F>F_α(1，N-2)，则推断β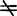0，并称Y_x与数量因子x线性相关显着。仅对这样的EYx用(48．4．1)₁式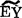_x作为它的线性模拟才是有意义的，并且可以认为EY_x=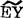_x。只在这种情形才有必要求出(48．4．1)₂式作为线性模拟(48．4．1)₁式的最小二乘估计。F_α(f₁，f₂)——f₁与f₂分别称为分子自由度和分母自由度——可以查“F检验的临界值(F_α)表”得到。回归分析的步骤如表48—2所示。

表48—2

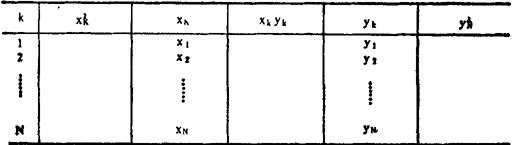
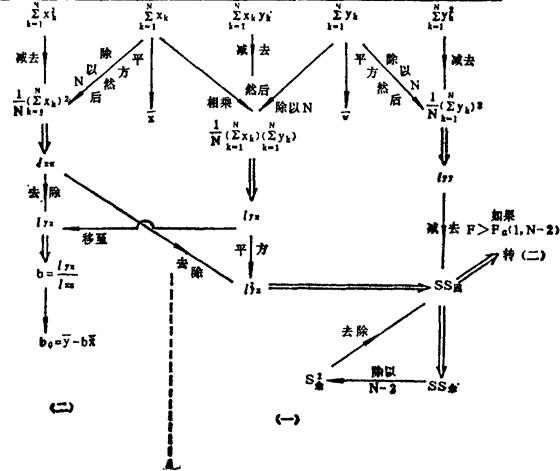
如果使用SHARP-5002计算器，则：

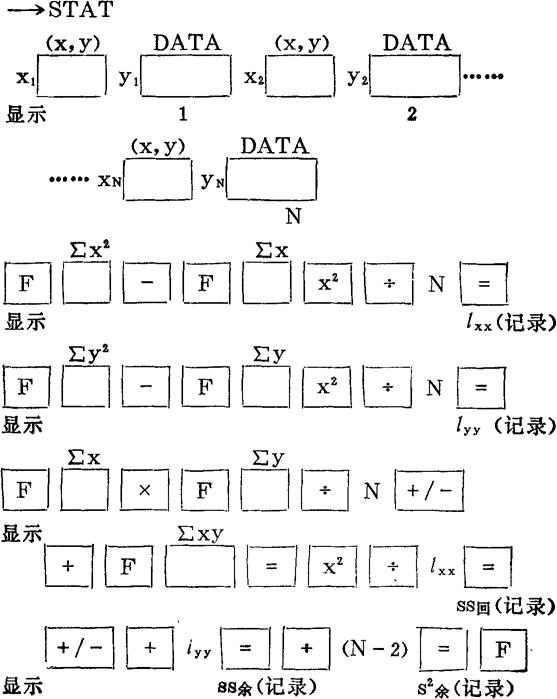
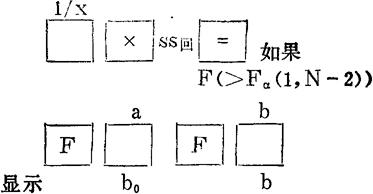
上述的线性回归分析以总体方差DY_x≡σ²，即不随x∈T改变为前提。下面写出总体标准差σ与β₀、β、EY_x的1-α置信区间以及总体Y_x的1-α取值区间：

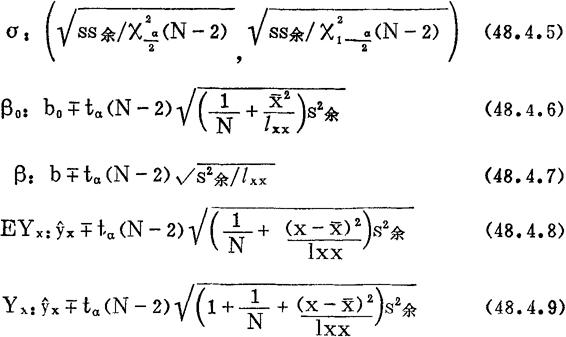
X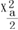(N-2)和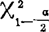(N-2)可以查“X²分布的上侧分位数(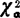)表”得到；t_α(N-2)可以查“t分布的双侧分位数(t_α)表”得到，N-2是自由度。(18．|．8)式和(48．4．9)式在线性模拟的最小二乘估计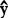_x=b₀+bx两侧随x∈〔x₁，x_N〕分别形成EY_x的1-α置信区域和总体族Y_x的1-α取值区域，它们在距离X越远的x处(即|x-X|越大)开口越大。

对于依赖于m个数量因子的总体族{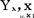=(x₁，x₂…，xm)^T∈T}，m个数量因子的取值有如下两种情况：(1)取值之间有依赖关系，或者人们不能控制只能记录。这种情况类似于m+1元总体(m个随机自变量，一个随机因变量)；(2)取值之间没有关系，并且可以由人们对其进行搭配(全面搭配或者正交搭配，后一种称为正交回归设计)。本章只研究第(1)种情况。

把样本观测值与数量因子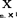的取值配合，借用m+1元总体的样本观测值的格式。

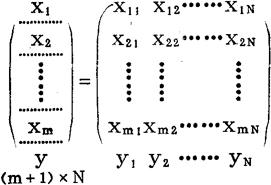
总体族的平均数EY_x的线性模拟：

用下列最小二乘法求β₀和β_j，j=1—m的估计值：

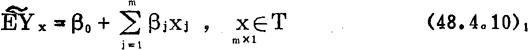
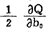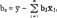由=0推出，将其代入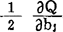=0，j=1—m，得到m元线性回归的正规方程组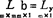：，其中：

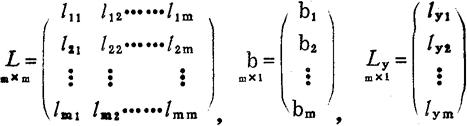
假设系数阵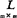的行列式不等于0，解得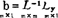

线性模拟(48．4．10)₁式的最小二乘估计⁽³⁾是：

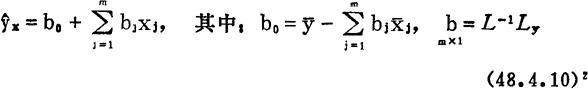
定义下列剩余平方和与回归平方和：

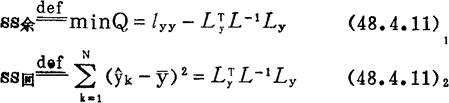
由以上二式可知；

按(48．4．10)₂式求得线性模拟(48．4．10)₁式的最小二乘估计的前提是下列的F>F_α(m，N—m—1)：

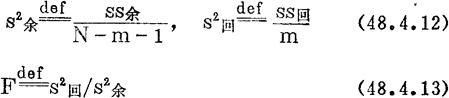
简单介绍正交回归设计：采用正交表使可以人为控制的m个数量因子的取值两两全面搭配，从而正规方程的系数阵成为对角阵，回归平方和也成为简单的∑求和，在形式上是一元线性的b=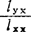与Ss回=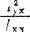=bl_xx随因子个数增多的简单增加：

(编者：刘长安 审者：孙尽善)