渐近展开法
逼近论和解析数论的重要工具。
其基本思想是利用一个简单函数系去逼近一个复杂的函数,并使之逼近到任意精确的程度。因此,渐近展开方法在理论和实际计算中都有重要应用。
设{φn(x)}(n=0,1,2,…)为一函数序列,它满足下列条件:φ1(x)=0(φ0(x)),φ2(x)=0(φ1(x)),…(x→∞),设存在一列常数C0,C1,C2,…使得函数f(x)有以下的估计
f(x)=o(φ0(x)), (x→∞);
f(x)=c0φ0(x)+o(φ1(x)), (x→∞);
f(x)=c0φ0(x)+c1φ1(x)+o(φ2(x)), (x→∞);
…………
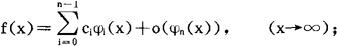
…………
显然,上式是一个逐次精密的过程,如果上式成立,则记
f(x)≈c0φ0(x)+c1φ1(x)+c2φ2(x)+…,
(x→∞)
并称右式为f(x)关于函数列{φn(x)}的渐近级数或渐近展开,例如,函数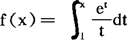 ,利用分部积分法,可以得到exf(x)关于函数列
,利用分部积分法,可以得到exf(x)关于函数列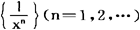 的渐近级数是
的渐近级数是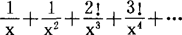 ,并有以下估计式成立
,并有以下估计式成立
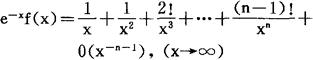
在渐近展开中,最简单最重要的是取φn(x)=x-n,(n=0,1,2,…)的情形,对此种情形,渐近展开的意义可表述如下:设函数F(x)与级数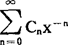 的第n个截断
的第n个截断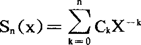 之差
之差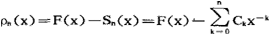 ,对于任意固定的n都满足条件
,对于任意固定的n都满足条件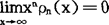 ,则称级数
,则称级数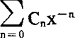 是函数F(x)的渐近展开或渐近级数,并记为
是函数F(x)的渐近展开或渐近级数,并记为
F(x)≈C0+C1X-1+C2X-2+…
显然,一个函数的渐近级数并不一定收敛到该函数,甚至它可以是发散的。渐近展开还有以下重要性质:(1)(唯一性)若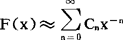 ,且
,且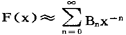 ,则必有Cn=Bn(n=0,1,2,…)(2)若
,则必有Cn=Bn(n=0,1,2,…)(2)若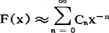 ,
,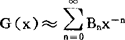 ,则
,则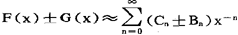 ,
,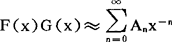 ,其中
,其中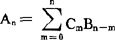 ;(3)若
;(3)若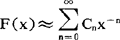 则
则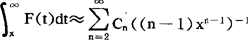 ;(4)若
;(4)若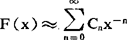 ,则
,则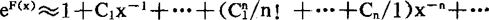 。
。
- 绝妙孙辛妇是什么意思
- 绝妙对联450是什么意思
- 绝妙无比的诗文书画是什么意思
- 绝妙的作品是什么意思
- 绝妙的姿态是什么意思
- 绝妙的文章是什么意思
- 绝妙的文辞是什么意思
- 绝妙的缝绣工艺是什么意思
- 绝妙的讽刺小品>——说朱熹《记孙觌事》是什么意思
- 绝妙的音乐是什么意思
- 绝妙的魔术家是什么意思
- 绝妙词是什么意思
- 绝妙近词是什么意思
- 绝娠是什么意思
- 绝嫩是什么意思
- 绝子是什么意思
- 绝子妈妈是什么意思
- 绝子绝孙是什么意思
- 绝孕是什么意思
- 绝孕穴是什么意思
- 绝学是什么意思
- 绝学无忧是什么意思
- 绝学无忧。是什么意思
- 绝完了是什么意思
- 绝宗是什么意思
- 绝密是什么意思
- 绝密公文是什么意思
- 绝密情报是什么意思
- 绝密文件是什么意思
- 绝密电报是什么意思
- 绝密邮件是什么意思
- 绝对是什么意思
- 绝对·相对是什么意思
- 绝对不会出差错是什么意思
- 绝对不会失误是什么意思
- 绝对不变式是什么意思
- 绝对不应期是什么意思
- 绝对不稳定是什么意思
- 绝对不等式是什么意思
- 绝对不能容忍是什么意思
- 绝对不能犯是什么意思
- 绝对不能让与的人权和基本不能让与的人权是什么意思
- 绝对专制时期是什么意思
- 绝对中立是什么意思
- 绝对主义是什么意思
- 绝对主义道德论是什么意思
- 绝对主权是什么意思
- 绝对义务是什么意思
- 绝对乏兴奋期是什么意思
- 绝对事件是什么意思
- 绝对人口过剩是什么意思
- 绝对价值是什么意思
- 绝对价值量是什么意思
- 绝对价格是什么意思
- 绝对优势是什么意思
- 绝对优势理论是什么意思
- 绝对优势策略是什么意思
- 绝对优势论是什么意思
- 绝对供给曲线是什么意思
- 绝对保护区是什么意思