条件概率

---

条件概率的定义 设两事件A，B，且P(A)＞0，则称

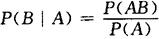
为事件A发生的条件下，事件B发生的条件概率．

条件概率与概率有相同的性质：

(1)对任一事件B，0≤P(B|A)≤1；

(2)P(Ω|A)=1；

(3)若B₁，B₂，…是两两互斥事件，则有

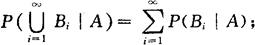
(4)对任意两事件B₁，B₂，有

P(B₁∪B₂|A)=P(B₁|A)+P(B₂|A)－P(B₁B₂|A)．

条件概率中的条件事件A起着样本空间的作用，被称为缩小的样本空间．

乘法定理(公式) 对事件A，B，且P(A)＞0，P(B)＞0，则有

P(AB)=P(A)P(B|A)，

P(AB)=P(B)P(A|B)；

推广：对事件A₁，A₂，…，A_n，且P(A₁A₂…A_n－1)＞0，则有

P(A₁A₂…A_n)=P(A₁)P(A₂|A₁)…P(A_n|A₁A₂…A_n－1)．

乘法公式是计算交事件概率的基本公式．

全概率公式和逆概率公式

1．全概率公式

(1)划分(分割)：设Ω为随机试验E的样本空间，B₁，B₂，…，B_n为E中的一组事件，如果①，i，j=1，2，…，n．②．则称｛B₁，B₂，…，B_n｝为样本空间Ω的一个划分(又叫分割，分划)．

若｛B₁，B₂，…，B_n｝为Ω的一个划分，则对每次试验，事件B₁，B₂，…，B_n中必有一个且仅有一个发生．

(2)全概率公式：设Ω是试验E的样本空间，A为E中的一个事件．｛B₁，B₂，…，B_n｝为Ω的一个划分，且P(B_i)＞0(i=1，2，…，n)，则有

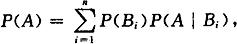
并称之为全概率公式．

概率论的重要问题之一就是希望从已知的比较简单的事件的概率，推算出未知的比较复杂的事件的概率．为此，人们在处理问题时，经常把一个复杂事件分解成若干个互斥的简单事件的并，再分别计算这些简单事件的概率，最后利用概率的可加性，得出复杂事件的概率．全概率公式就是起着这种重要作用的基本公式．它在实践中有着广泛的应用．

2．逆概率公式(贝叶斯公式)

通常称概率P(B_i|A)为P(A|B_i)的逆概率，自然就称计算概率P(B_i|A)的公式为逆概率公式．

设Ω是试验E的样本空间，A为E中的一个事件，｛B₁，B₂，…，B_n｝为Ω的一个划分，且P(A)＞0，P(B_i)＞0(i=1，2，…，n)，则有

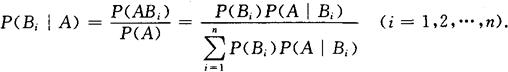
这就是逆概率公式(贝叶斯公式)．